SkyCiv'de eğitimin önemli olduğuna inanıyoruz, bu nedenle yeni nesil mühendislerin yapısal mühendisliği öğrenmesine yardımcı olmaya kararlıyız. Bu misyonun bir parçası olarak, yapısal mühendislik yazılımının kara kutusunu açan Moment Dağılım Yöntemi El Hesaplama Raporları geliştiriyoruz, kullanıcılarımızın meraklı zihinlerine açığa çıkarmak. Mühendisler bir şeyin nasıl ve neden böyle olduğunu bilmek ister, ve genellikle bunu öğrenmenin en iyi yolu, kendi kendinize çözmeye çalışmak ve çözümünüzü eksiksiz ve doğru olanla karşılaştırmaktır.. Raporlarımızın okunabilirliğini, hesaplamaları tekrar kontrol etmek için gereken ayrıntı düzeyiyle dengeliyoruz., adım adım. Bu, mühendislik uygulamaları için temeldir ve kullanıcılara eğitimlerine değer katan araçlar sağlamaya devam edeceğiz., İş, ve yaşıyor.
İstediğin şey tarafından yönlendiriliyoruz: kullanıcılarımızdan en çok talep edilen özelliklerden biri belirsiz kirişler için elle hesaplamalar olmuştur.. Bu özelliğin artık yayında olduğunu duyurmaktan gurur duyuyoruz: mevcut Öğrenci, Temel ve Profesyonel kullanıcılar şunları yapabilir: şimdi dene. Menteşesiz belirsiz kirişler için, düşey ve moment reaksiyonları Moment Dağılım Yöntemi kullanılarak çözülür..
Moment Dağılım Yöntemi El Hesaplama modülü, aşağıdaki gibi bir kiriş için el hesaplamalarını kolayca gösterecektir:
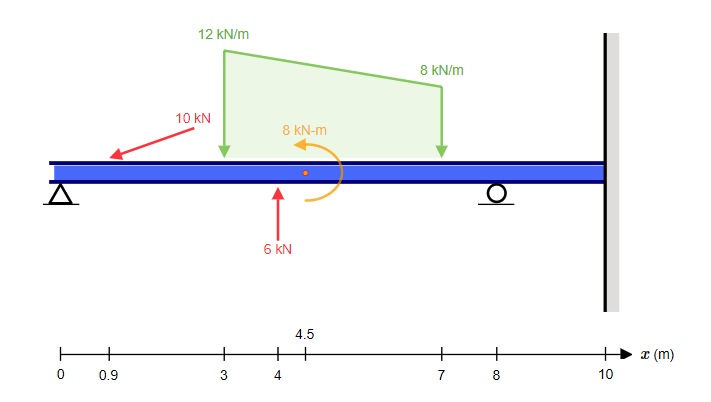
Mevcut kullanıcılar, Beam'deki statik olarak belirli yapılar için el hesaplamalarına erişmeye aşina olacaklardır., SkyCiv'de yeniyseniz veya henüz el hesaplamalarını bulmayı denemediyseniz, bizim dokümantasyon süreç boyunca size rehberlik edebilir.
Moment Dağılım Yöntemi
Moment Dağılım Yöntemi (MDM), Hardy Cross tarafından icat edildi, sadeliği açısından son derece güçlüdür ve ASCE dergisi tarafından ilk kez yayınlandığından beri yoğun bir şekilde kullanılmaktadır. 1930. Basitliğinin bir kısmı, eğilme momenti diyagramının, her bir segment için süreksizlik denklemlerini hesaplamaya gerek kalmadan üst üste binme kullanılarak grafiksel olarak çizilebilmesinde yatmaktadır.. Karmaşık yapılar, FEM gibi diğer yöntemlere kıyasla nispeten daha kolay çözülebilir, Sanal Yer Değiştirme Yöntemi, veya süreksizlik denklemlerini çözme. MDM, kirişler ve çerçeveler gibi çeşitli 2B yapılarda kullanılabilir.
Hardy Cross, el hesaplamasının herhangi bir yapı mühendisi için vazgeçilmez bir egzersiz olduğu bir dönemde yapısal bir mühendisdi.. Yapıları hesaplama sürecini sayısız kez tekrarladıktan sonra, aslında aynı hesaplamaları defalarca yaptığını fark etti.. Bu, Cross'un karmaşık yapıların aslında basit yapıların ve basit yapıların kombinasyonları olduğu teorisini keşfetmesine yol açtı., Bu basit yapılar, karmaşık yapıyı aynı analitik çözümle oluşturmak için bir araya getirilebilir. Basit yapıların çözülmesi kolaydır, Formüller belirsiz olsalar bile türetilmesi yeterince kolaydı, süperpozisyon ve Sanal Kuvvet Yöntemi sayesinde. Cross, bu basit yapıların tablolarını oluşturdu ve teorisini çeşitli şekillerde test etmeye başladı..
Sabit Son Moment Denklemleri
Moment Dağılım Yöntemi, her bir segmentin sonundaki momentler için denklemleri aramak için ortak yükleme durumlarının tablolarını kullanır.. Bu tablolar dokümantasyonumuzda bulunabilir. eğilme momenti diyagramlarının hesaplanması ve yalnızca MDM'nin kullanıldığı temeli oluşturmakla kalmaz, aynı zamanda basit eğilme momenti hesaplamaları için harika bir referanstır. Buna bakmanın basit bir yolu, MDM, kirişi parçalara ayırır, ve BMD'yi hesaplamak için bu basit denklemleri kullanır.
Alternatif yöntemler
Eğilme momenti diyagramının hesaplanması başka yollarla da elde edilebilir, daha önce yazdığımız süreksiz denklemleri kullanmak gibi İşte.
Örnek Rapor



