Was ist P-Delta-Analyse?? | SkyCiv Engineering

Die P-Delta-Analyse ist eine Art der Analyse, die besonders wichtig ist, um mehrstöckige Gebäudestrukturen mit Schwerkraft seitlich zu verschieben. In diesem Artikel, SkyCiv Online-Engineering-Software wird die einfache Theorie hinter P-Delta-Effekten diskutieren und Ihnen helfen, die Bedeutung einer solchen Analyse bei der Modellierung Ihrer Strukturen zu verstehen.

Was sind P-Delta-Effekte??

Natürlich, Jedes Strukturmodell wird beim Laden ausgelenkt. Eine abgelenkte Struktur kann auf signifikante Sekundärmomente stoßen, da die Enden der Elemente ihre Position geändert haben. Um dies zu veranschaulichen, Betrachten Sie das unten gezeigte einfache Beispiel für eine freitragende Säule: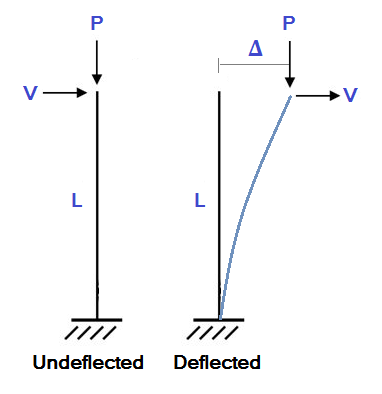

In diesem Beispiel, Eine Säule der Länge L trifft auf eine axiale Belastung (P.) und eine seitliche Belastung (V ). In einer linearen statischen Standardanalyse würden wir die seitliche Auslenkung berechnen (Δ) wie: [Mathematik] \Delta = dfrac{ML ^ 2}{3NEIN} = dfrac{VL ^ 3}{3NEIN} \Text{ da M = VL} [Mathematik] Beachten Sie, dass bei einer linearen statischen Analyse die seitliche Auslenkung erfolgt, Δ, hängt von der Querbelastung ab (V ). Jedoch, wenn die Säule einer axialen Belastung ausgesetzt ist (P.), dann würde die Säule nicht noch mehr ablenken? Dies ist offensichtlich, da die axiale Last ein sekundäres Moment mit einem Wert von P × Δ induzieren würde. Um dies zu veranschaulichen, Lassen Sie uns die Momente um die Basis der Spalte zusammenfassen: [Mathematik] \Summe{M.}=(V mal L.) + (P times Delta)= VL + P Delta \\\\ M_{1} = VL \\\\ M_{2} = P Delta [Mathematik] Hier M.₁ ist auf die seitliche Punktbelastung zurückzuführen, M.₂ ist auf die axiale Belastung zurückzuführen. Jeder dieser Momente trägt unterschiedlich zur seitlichen Auslenkung bei (Sie können die Auslegerformeln für die Endauslenkung aufgrund einer Punktlast und eines Moments nachschlagen, jeweils für diese Formeln): [Mathematik] \Delta_{1} = dfrac{M_{1}L ^ 2}{3NEIN} = dfrac{VL ^ 3}{3NEIN} \\\\ \Delta_{2} = dfrac{M_{2}L ^ 2}{2NEIN} = dfrac{P Delta L ^ 2}{2NEIN} [Mathematik] Also wirklich, die gesamte seitliche Auslenkung wäre näher an: [Mathematik] \Delta_{Neu} = Delta_{1} + \Delta_{2} = dfrac{VL ^ 3}{3NEIN} + \dfrac{P Delta L ^ 2}{2NEIN} [Mathematik] Wir können das im Vergleich zum ursprünglichen Auslenkungswert sehen, Auf der rechten Seite befindet sich ein zusätzlicher Term in Bezug auf P und Δ. Wenn P oder Δ signifikante Werte sind, Die standardmäßige lineare statische Analyse würde die Durchbiegung der Säule unterschätzen. Es sollte jetzt offensichtlich sein, dass eine P-Delta-Analyse nach dem sekundären Moment benannt ist PD. Deshalb, P-Delta-Effekte werden durch geometrische Nichtlinearität verursacht. Deshalb, Eine P-Delta-Analyse wird oft als a bezeichnet Nichtlineare Analyse. Eine ordnungsgemäße P-Delta-Analyse würde den obigen Prozess weiterhin wiederholen, um den Wert von Δ zu aktualisieren_Neu.

Wann muss ich mir Gedanken über die Durchführung einer P-Delta-Analyse machen??

Die gute Nachricht ist das SkyCiv Structural 3D kann jetzt eine P-Delta-Analyse für Sie durchführen. P-Delta-Effekte treten normalerweise in hohen Strukturen auf, die aufgrund von Wind oder anderen Kräften Schwerkraftbelastungen und seitlichen Verschiebungen ausgesetzt sind. Wenn die seitliche Verschiebung und / oder die vertikalen axialen Belastungen durch die Struktur signifikant sind, Eine P-Delta-Analyse sollte durchgeführt werden, um die Nichtlinearitäten zu berücksichtigen. In vielen Fällen, eine lineare statische Analyse kann stark unterschätzen Verschiebung (unter anderen Ergebnissen) im Vergleich zu einem P-Delta (Nicht linear) Analyse. Die Bedeutung einer nichtlinearen P-Delta-Analyse wird im folgenden Beispiel veranschaulicht. Der mehrstöckige Rahmen des Gebäudes ist 20 m hoch, Jedes Stockwerk ist 5 m hoch. Die Säulen sind vollständig an der Basis mit verteilten Lasten auf jeder Ebene befestigt. zusätzlich, Im obersten Stockwerk befinden sich vertikale Lasten, und das Eigengewicht wird berücksichtigt, damit Schwerkraftlasten simuliert werden können. Da ist auch ein relativ klein seitliche Belastung der Seite der Struktur.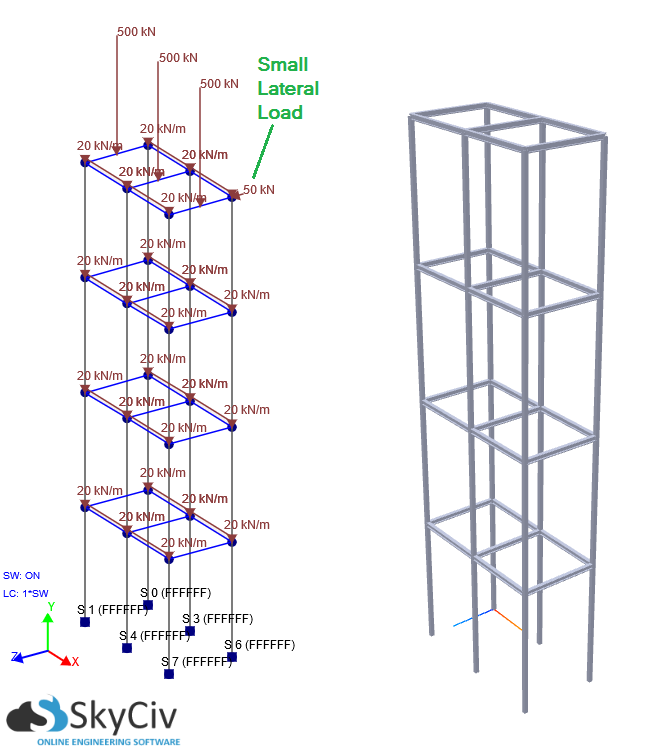

Vergleichen wir unter diesen Bedingungen die Ergebnisse zwischen einem linearen und einem P-Delta (Nicht linear) Analyse:

	lineare	P-Delta (Nicht linear)	% Unterschied
Maximale Gesamtverschiebung	254 mm	353 mm	+ 39%
Maximale vertikale Reaktion	629 kN	668 kN	+ 6%
Max Moment Reaktion	42 kN-m	60 kN-m	+ 43%

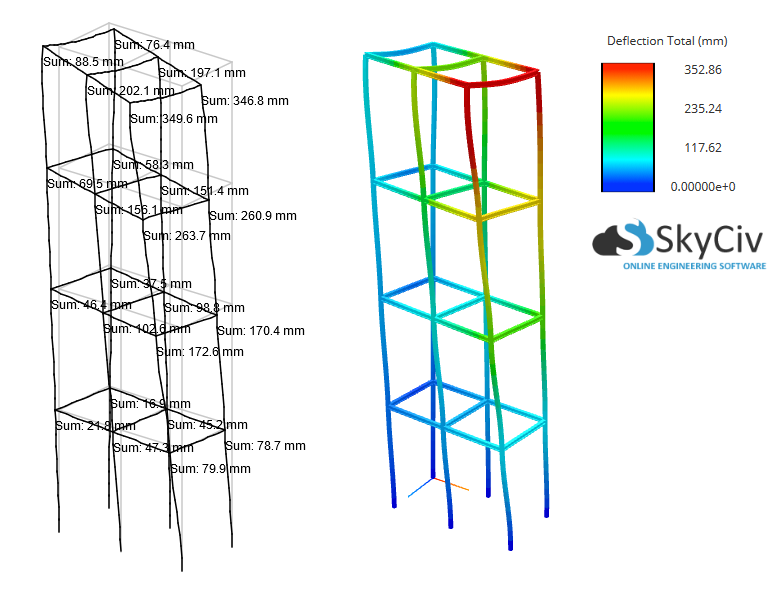Es ist klar, dass P-Delta-Effekte bei dieser Struktur eine äußerst wichtige Rolle spielen, Das Erhöhen der maximalen Durchbiegung und des maximalen Moments ergibt sich um ungefähr 40%! So, Eine lineare statische Analyse ist in einem solchen Fall unzureichend. Zusammenfassend, Die P-Delta-Analyse ist der linearen statischen Analyse vorzuziehen, da sie unvorhergesehene Nichtlinearitäten in Ihrem Modell berücksichtigt. Sie können verwenden SkyCiv Structural 3D um schnelle und effektive P-Delta-Analysen an Ihren Modellen durchzuführen; einfach auswählen "P-Delta-Analyse" beim Klicken "Lösen." Lassen Sie die Software die Arbeit für Sie erledigen, sodass Sie sich nur um das Design kümmern müssen!