Chez SkyCiv, nous croyons que l'éducation est importante, nous nous engageons donc à aider la prochaine génération d'ingénieurs à apprendre l'ingénierie structurelle.. Dans le cadre de cette mission, Dans le cadre de cette mission, l'exposer aux esprits curieux de nos utilisateurs. Les ingénieurs aiment savoir comment et pourquoi quelque chose est comme ça, et souvent, la meilleure façon d'apprendre cela est d'essayer de le résoudre vous-même et de comparer votre solution à une solution complète et correcte.. Nous équilibrons la lisibilité de nos rapports avec le niveau de détail requis pour vérifier les calculs, pas à pas. Ceci est fondamental pour la pratique de l'ingénierie et nous continuerons à fournir aux utilisateurs des outils qui ajoutent de la valeur à leur formation., travailler, Dans le cadre de cette mission.
Nous sommes motivés par ce que vous voulez: l'une des fonctionnalités les plus demandées par nos utilisateurs était les calculs manuels pour les poutres indéterminées. Nous sommes fiers d'annoncer que cette fonctionnalité est maintenant disponible: étudiant actuel, Les utilisateurs de base et professionnels peuvent Essayez-le maintenant. Pour poutres indéterminées sans charnières, les réactions verticales et de moment sont résolues en utilisant la méthode de distribution des moments.
Dans le cadre de cette mission, affichera facilement les calculs manuels pour une poutre comme celle-ci:
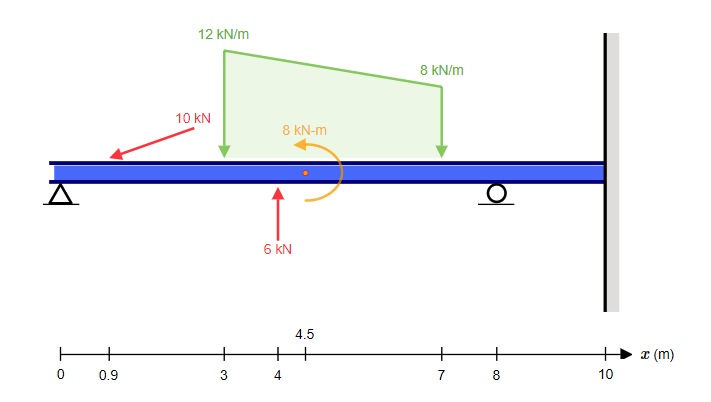
Cependant, les utilisateurs existants seront familiarisés avec l'accès aux calculs manuels pour les structures statiquement déterminées dans Beam, si vous êtes nouveau sur SkyCiv ou si vous n'avez pas encore essayé les calculs manuels trouvés, notre Documentation peut vous guider tout au long du processus.
Méthode de distribution des moments
Méthode de distribution des moments (MDM), inventé par Hardy Cross, est extrêmement puissant dans sa simplicité et a été largement utilisé depuis sa première publication par la revue ASCE dans 1930. Une partie de sa simplicité réside dans la façon dont le diagramme du moment de flexion peut être dessiné graphiquement en utilisant la superposition sans avoir besoin de calculer les équations de discontinuité pour chaque segment. Les structures complexes peuvent être résolues relativement facilement par rapport à d'autres méthodes telles que FEM, la méthode de déplacement virtuel, ou résoudre des équations de discontinuité. MDM peut être utilisé sur une variété de structures 2D comme les poutres et les cadres.
Hardy Cross était un ingénieur en structure à une époque où le calcul manuel était un exercice indispensable pour tout ingénieur en structure.. Après avoir répété le processus de calcul des structures d'innombrables fois, il a reconnu qu'il effectuait essentiellement les mêmes calculs encore et encore.. Cela a conduit Cross à explorer une théorie selon laquelle les structures complexes étaient en fait des combinaisons de structures simples et, ces structures simples pourraient être assemblées pour créer la structure complexe avec la même solution analytique. Les structures simples sont faciles à résoudre, les formules étaient assez faciles à dériver même si elles étaient indéterminées, grâce à la superposition et à la méthode Virtual Force. Cross a créé des tableaux de ces structures simples et s'est mis à tester sa théorie de différentes manières..
Equations des moments de fin fixes
La méthode de distribution des moments utilise des tableaux de cas de chargement courants pour rechercher les équations des moments aux extrémités de chaque segment. Ces tableaux se trouvent dans notre documentation pour calcul des diagrammes de moment de flexion et pas seulement la base sur laquelle le MDM est utilisé, mais est également une excellente référence pour les calculs simples de moment de flexion. Une façon simple de le regarder est, le MDM divise la poutre en segments, et utilise ces équations simples pour calculer la DMO.
Méthodes alternatives
Le calcul du diagramme des moments de flexion peut être réalisé de différentes manières, comme utiliser des équations discontinues dont nous avons parlé précédemment ici.
Exemple de rapport



