Ασύμμετρα τμήματα

Οι ασύμμετρες τομές δεν είναι συμμετρικές στον κατακόρυφο άξονα y ή στον οριζόντιο άξονα z ή, σε ορισμένες περιπτώσεις, οποιονδήποτε άξονα. Παραδείγματα ασύμμετρων τομών είναι οι γωνίες και οι τομές Ζ.

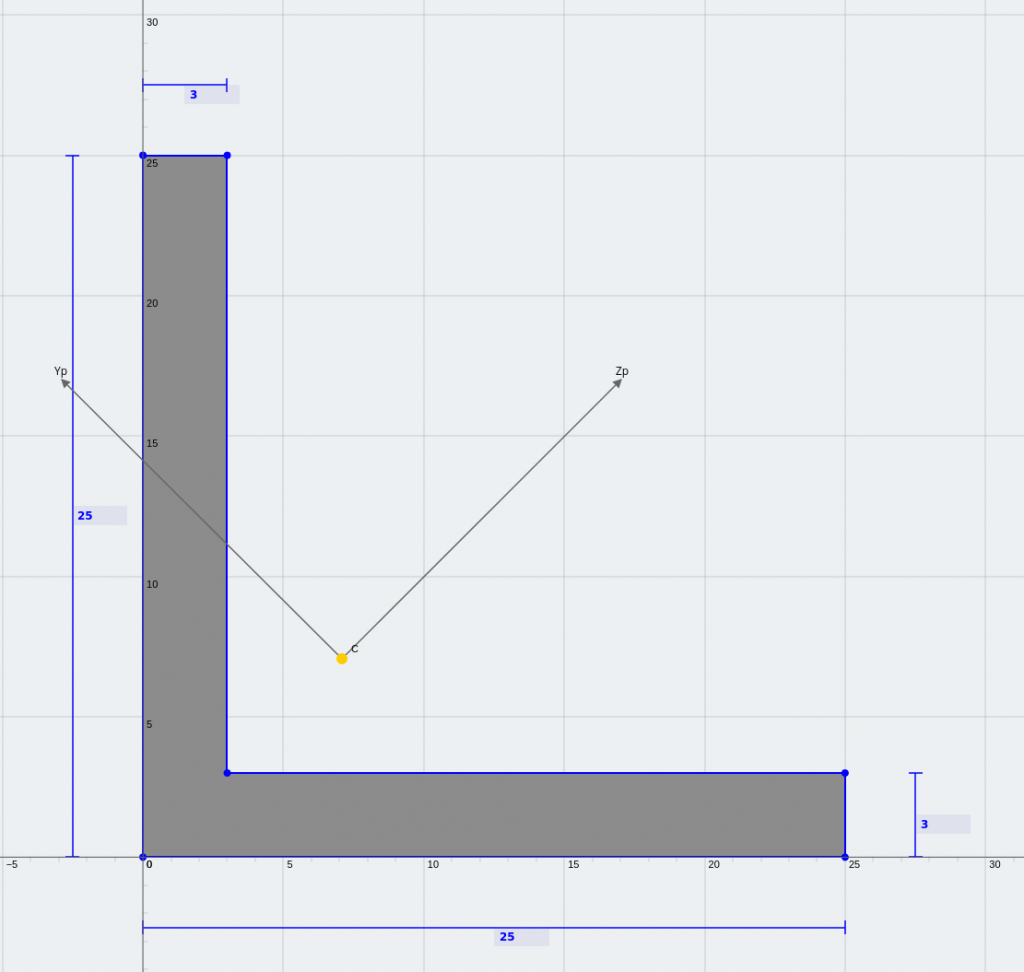
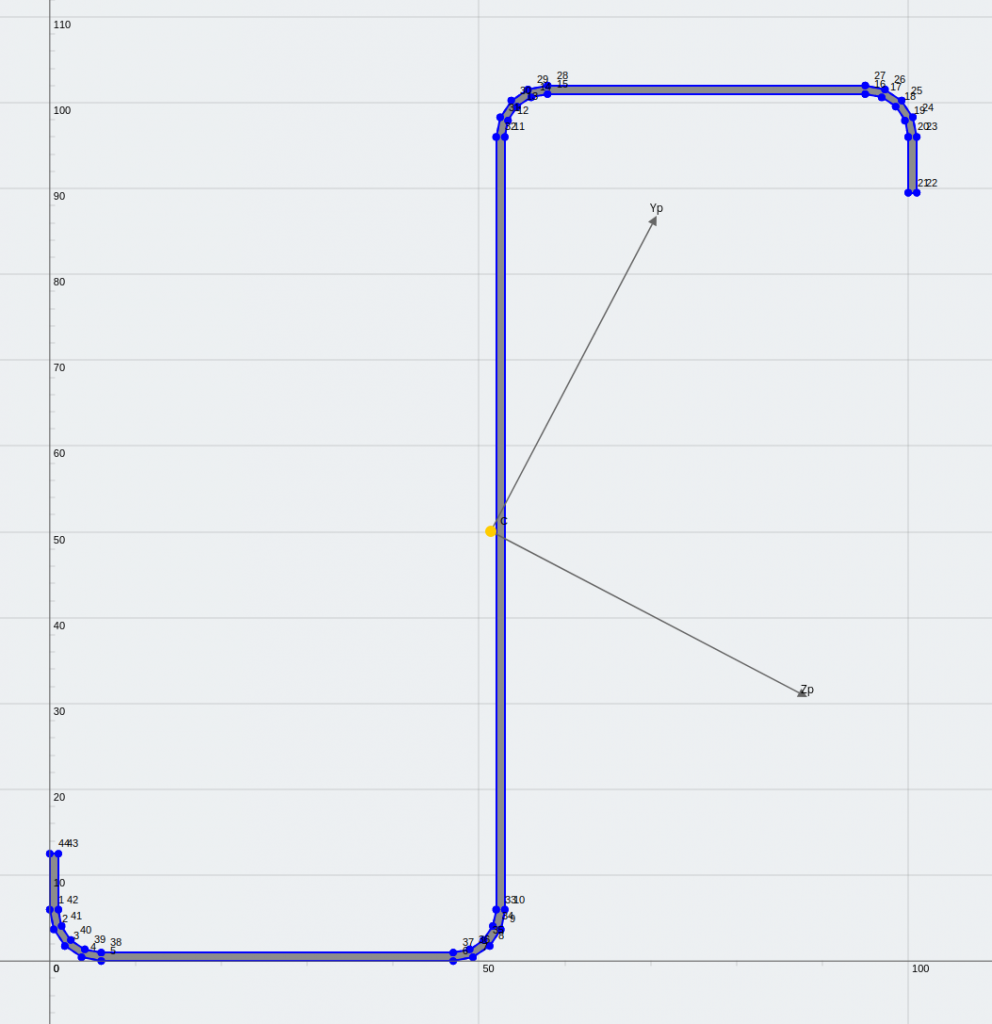
Τι είναι οι ασύμμετρες τομές (Τι είναι οι ασύμμετρες τομές)

Δοκοί με ασύμμετρες διατομές συμπεριφέρονται διαφορετικά σε δοκούς με δισυμμετρία στην κάμψη. Ακόμα κι αν η δέσμη έχει ισοδύναμη ακαμψία στον κάθετο άξονα, δεν θα συμπεριφέρεται όπως το RHS και το I Shape.

Σε αυτό το παράδειγμα θα δείξω τη συμπεριφορά τους με μια απλή θήκη φόρτωσης: κάθετο ομοιόμορφα κατανεμημένο φορτίο.

Ανάλυση

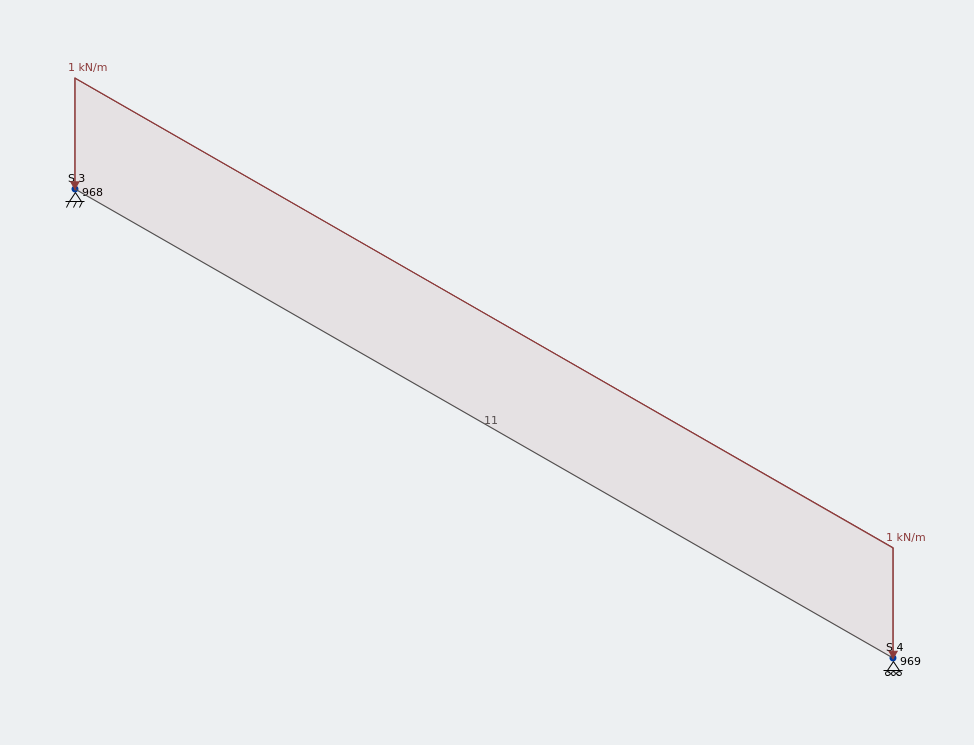
Μοντέλο πλαισίου ενός 1.5 m ίση γωνία κάτω από κάθετο UDL

Έχω εφαρμόσει ομοιόμορφα κατανεμημένο φορτίο 1kN/m σε όλο το μήκος αυτού 1.5 m ίση γωνία.

Αν ήθελα να ελέγξω την απόκλιση στο μέσο διάστημα αυτής της δοκού θα μπορούσα πολύ εύκολα. Το μόνο που θα χρειαζόμουν θα ήταν η δεύτερη στιγμή της περιοχής, και ο τυπικός τύπος μέγιστης εκτροπής για απλώς υποστηριζόμενη δέσμη. Ένας γρήγορος υπολογισμός χρησιμοποιώντας το SkyCiv Section Builder και αποκτώ εύκολα τις ιδιότητες της ενότητας.

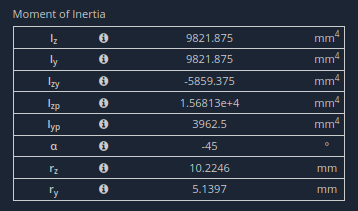
Πίνακας ιδιοτήτων ενότητας από το SkyCiv Section Builder

Iz είναι 9821.9 mm στην 4η ισχύ. Το τμήμα είναι δομικό χάλυβα με E = 200 GPa.

Κοιτάξτε τι συμβαίνει όταν το υπολογίζω με FEA στο SkyCiv Structural 3D.

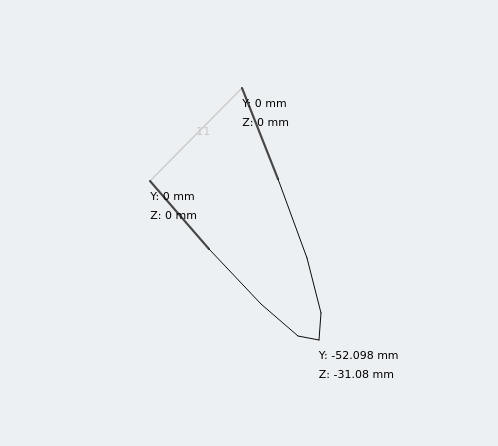
Μετατόπιση ίσης γωνίας υπό φόρτωση

Το τμήμα ίσης γωνίας έχει δύο στοιχεία εκτροπής! Ανάλυση της εκτροπής μιας απλά υποστηριζόμενης δέσμης χρησιμοποιώντας μια δι-συμμετρική τομή χρησιμοποιώντας τον προηγούμενο υπολογισμό, αυτή θα ήταν μια απολύτως αποδεκτή προσέγγιση για έναν γρήγορο έλεγχο. Αλλά για τις ασύμμετρες ενότητες χρειαζόμαστε μια άλλη πληροφορία.

Η γωνία α

Παρατηρήστε ότι στην ενότητα ιδιότητες παραπάνω, η τιμή για το α είναι μη μηδενική.

Αυτό σημαίνει ότι ο κύριος άξονας δεν είναι παράλληλος με έναν από τους γεωμετρικούς άξονες.

Για να καταδείξετε την επίδραση της περιστροφής του άξονα στις υπολογισμένες τιμές ακαμψίας, Έχω σχεδιάσει κάτω από την ακαμψία στον οριζόντιο και κάθετο άξονα καθώς περιστρέφεται το σύστημα συντεταγμένων.

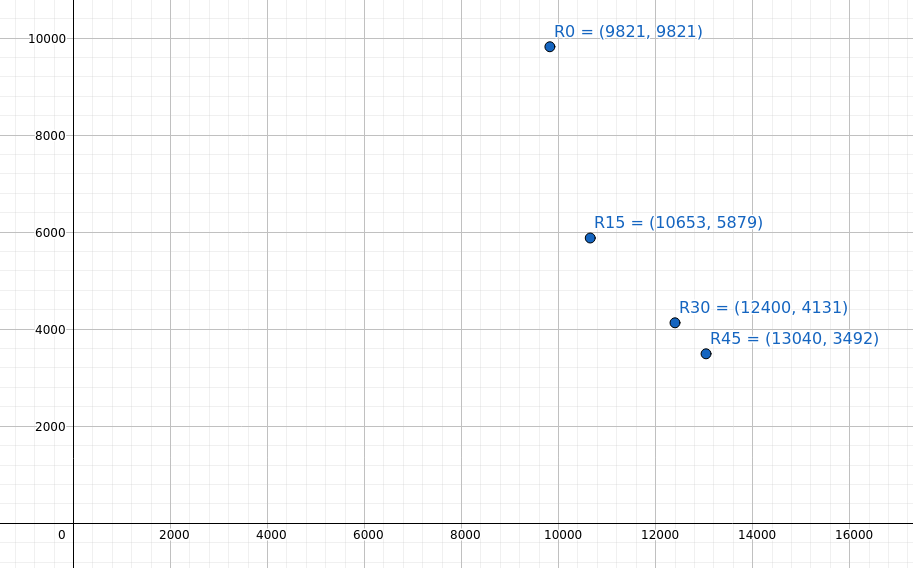
Ακαμψία 25x25x3 EA μετά την περιστροφή του συστήματος συντεταγμένων

Σημειώστε τη μη γραμμική καμπύλη που σχηματίζεται καθώς το σύστημα συντεταγμένων περιστρέφεται 15, 30 και 45 βαθμούς. Αυτή η καμπύλη θα είναι μοναδική για το τμήμα.

Γιατί λοιπόν συμβαίνει αυτό?

Ένας λέκτορας μου είπε μια φορά ότι τα φορτία ακολουθούν τα πιο σκληρά μέρη της δομής. Σε αυτήν την περίπτωση, το φορτίο μεταφέρεται από τον πιο σκληρό άξονα (ο κύριος κύριος άξονας).

Η σωστή προσέγγιση

Ο σωστός τρόπος υπολογισμού των αποτελεσμάτων εκτροπής περιλαμβάνει πρώτα τη μετατροπή όλων των φορτίων στους κύριους άξονες, στη συνέχεια, υπολογίζοντας τις εκτροπές με βάση τη δεύτερη στιγμή της περιοχής κατά μήκος των κύριων αξόνων. Για να αποδείξω ότι αυτή είναι πράγματι η σωστή προσέγγιση, επικύρωσα την απάντηση χρησιμοποιώντας έναν υπολογισμό με το χέρι, και για να γίνει αυτό λίγο πιο ενδιαφέρον, με ένα μοντέλο της δέσμης χρησιμοποιώντας ένα στοιχείο πλαισίου και, ένα μοντέλο χτισμένο από κελύφη. Με αυτόν τον τρόπο δεν υπάρχει αμφιβολία ότι οι μετατοπίσεις που είδαμε πριν είναι πράγματι σωστές.

Εδώ είναι το μοντέλο που δημιούργησα.

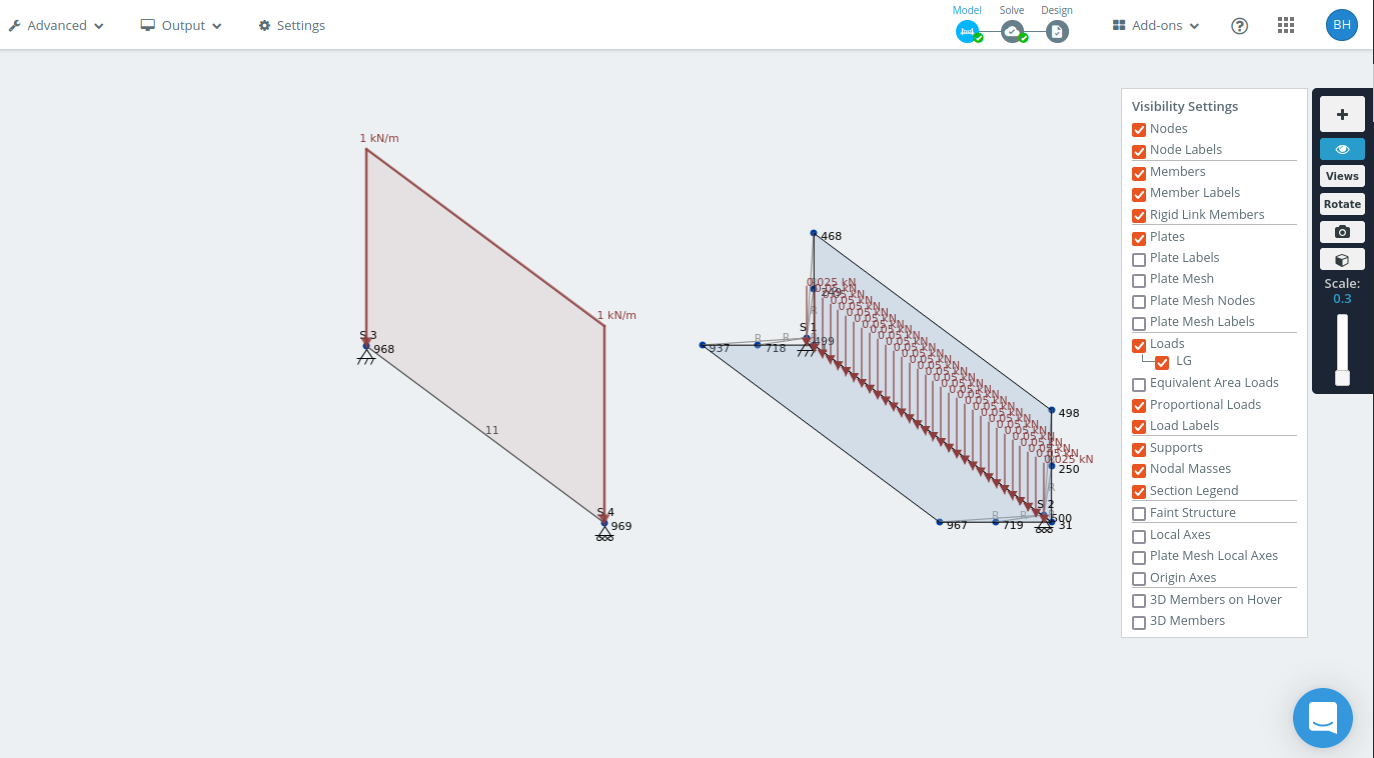
Μοντέλο πλαισίου και μοντέλο κελύφους του 1.5 m γωνία

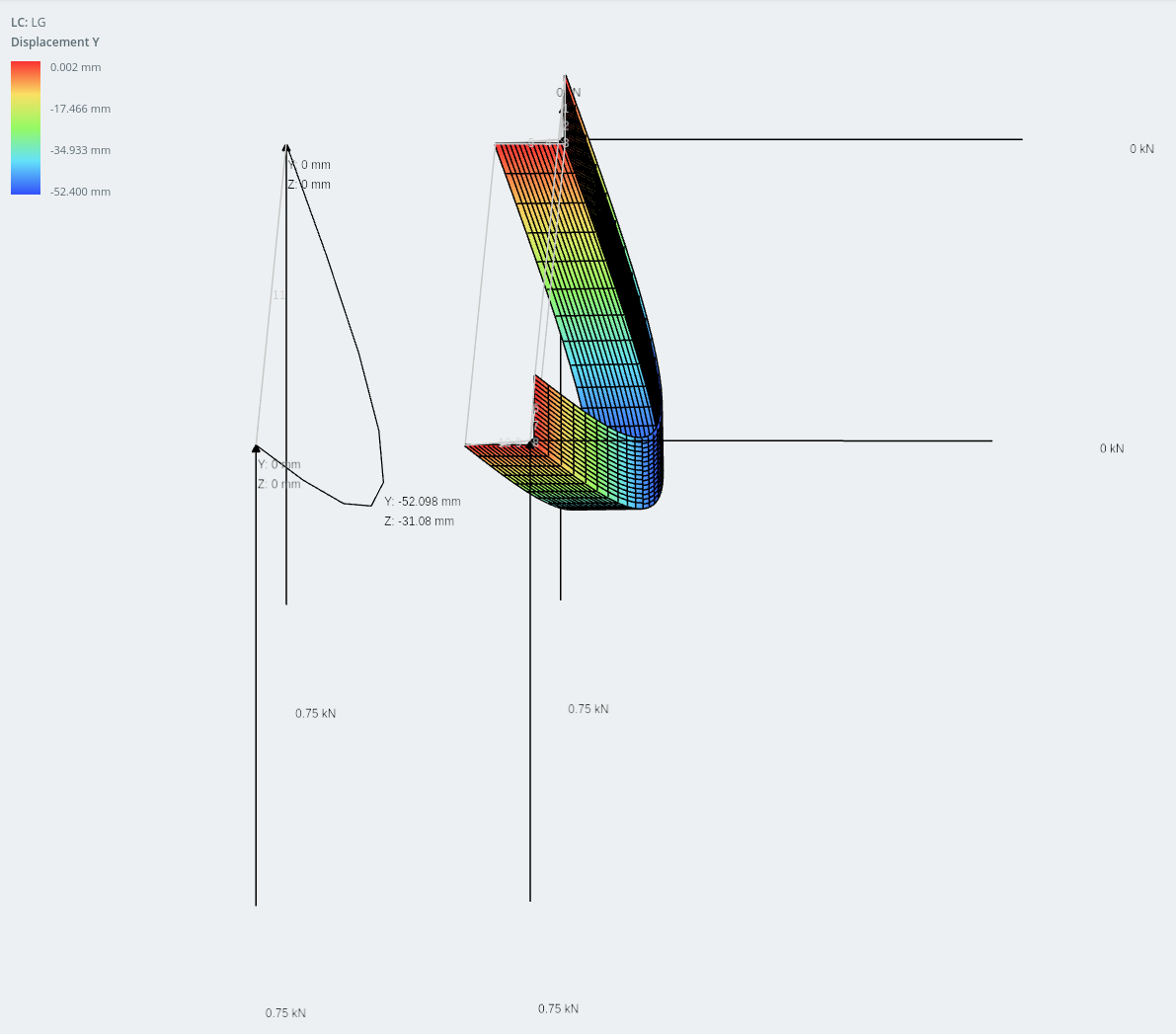
Μετατόπιση στην κάθετη κατεύθυνση

Η διαφορά στα αποτελέσματα μεταξύ των δύο μοντέλων είναι εξαιρετικά κοντά: στα πλαίσια 1% του άλλου.

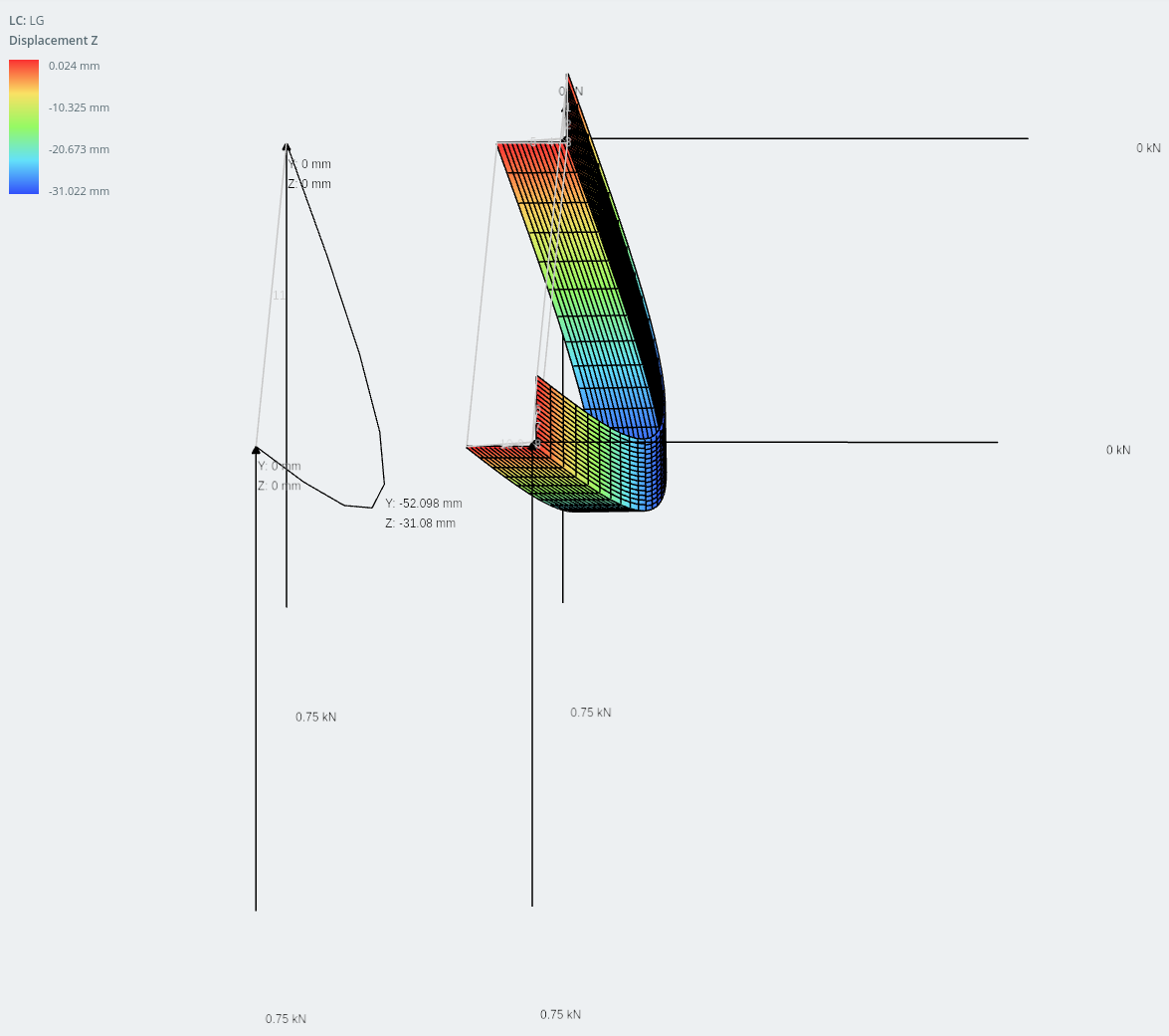
Μετατόπιση στην οριζόντια κατεύθυνση.

Και επιβεβαιώνονται από τους υπολογισμούς χειρός παρακάτω.

Γιατί θα θέλατε να χρησιμοποιήσετε αυτές τις ενότητες?

Στον μηχανικό αρέσει να σχεδιάζει δομές που είναι ελαφριές και αποδοτικές, Ωστόσο, μερικές φορές υπάρχουν περιορισμοί στη μορφή δομικών στοιχείων, συνήθως οφείλεται σε αποφάσεις σχεδιασμού από άλλους. Αυτός ο περιορισμός στη μορφή θα μπορούσε να οφείλεται σε πολλούς λόγους, μπορεί να συμβαίνει επειδή ένας αρχιτέκτονας θέλει να κρύψει δομικά στοιχεία για αισθητικούς λόγους, ή για συμμόρφωση με τους τοπικούς νόμους σχεδιασμού. Μπορεί να υπάρχουν περιορισμοί λόγω της τοπικής παραγωγικής ικανότητας ή απλώς της διαθεσιμότητας και του κόστους των πρώτων υλών. Το κόστος κατασκευής και η επίστρωση μπορεί επίσης να διαδραματίσουν σημαντικό ρόλο. Ωρες ωρες, είμαστε κολλημένοι με αυτά που έχουμε.

Όταν υπάρχει επιλογή, το τμήμα μπορεί να επιλεγεί επειδή έχει ορισμένα πλεονεκτήματα. Πάρτε για παράδειγμα ενότητες Ζ, τα οποία συνήθως φαίνονται να υποστηρίζουν κεκλιμένα φύλλα χάλυβα με προφίλ. Τυπικά για μικρές κεκλιμένες γωνίες στέγης, Τα κανάλια είναι πιο αποτελεσματικά επειδή τα φορτία βαρύτητας προκαλούν μόνο μικροσκοπικές στιγμές για τον ασθενή άξονα. Αυτές οι στιγμές αυξάνονται καθώς αυξάνεται η κλίση της οροφής και σε μια ορισμένη κλίση, Τα τμήματα Ζ γίνονται πιο αποτελεσματικά.

Για επίδειξη, διαμόρφωσα το τμήμα με το χείλος ως χαλύβδινη δοκό 1,5 μέτρων. Τι είναι οι ασύμμετρες τομές.

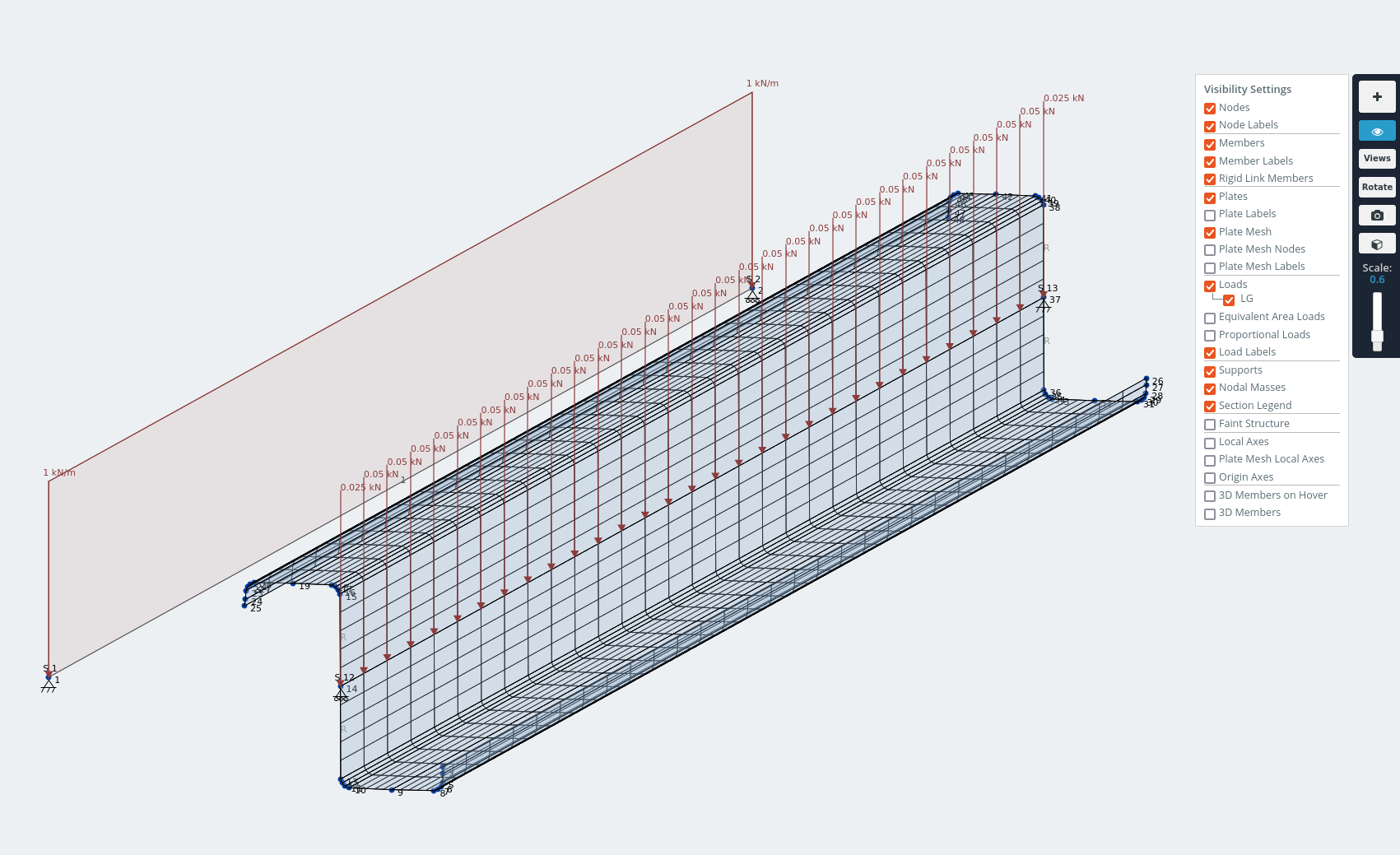
Μοντέλο τμήματος με χείλη-Ζ με κατανεμημένο φορτίο 1kN/m που εφαρμόζεται μέσω του κέντρου διάτμησης.

Η μετατόπιση στον άξονα z αντιτίθεται στην εσωτερική διάτμηση της επένδυσης της οροφής υπό φορτία βαρύτητας.

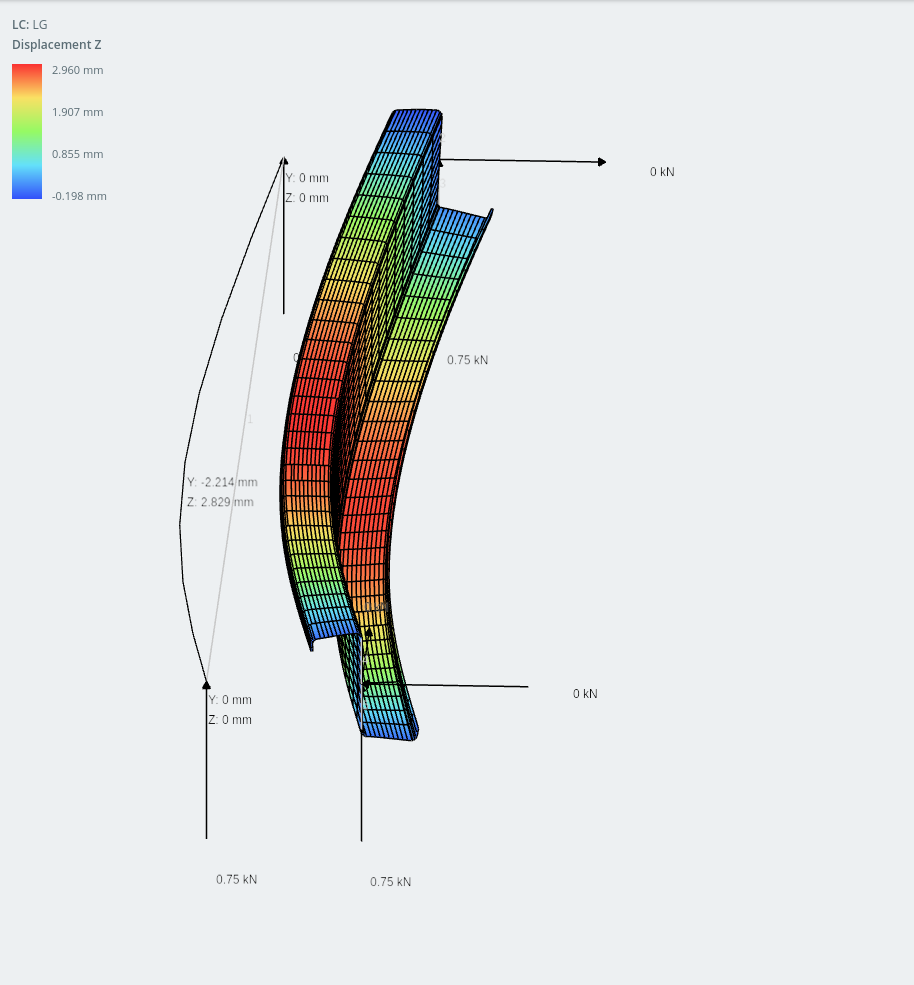
μοντέλο πλαισίου με λιπ-Ζ τμήμα και μοντέλο κελύφους (οριζόντια μετατόπιση που φαίνεται στις πλάκες)

Καταπληκτικά, η μετατόπιση στον άξονα y (κατακόρυφος) είναι στην πραγματικότητα μικρότερη από την οριζόντια. Τι είναι οι ασύμμετρες τομές, Τι είναι οι ασύμμετρες τομές, Τι είναι οι ασύμμετρες τομές, Τι είναι οι ασύμμετρες τομές!

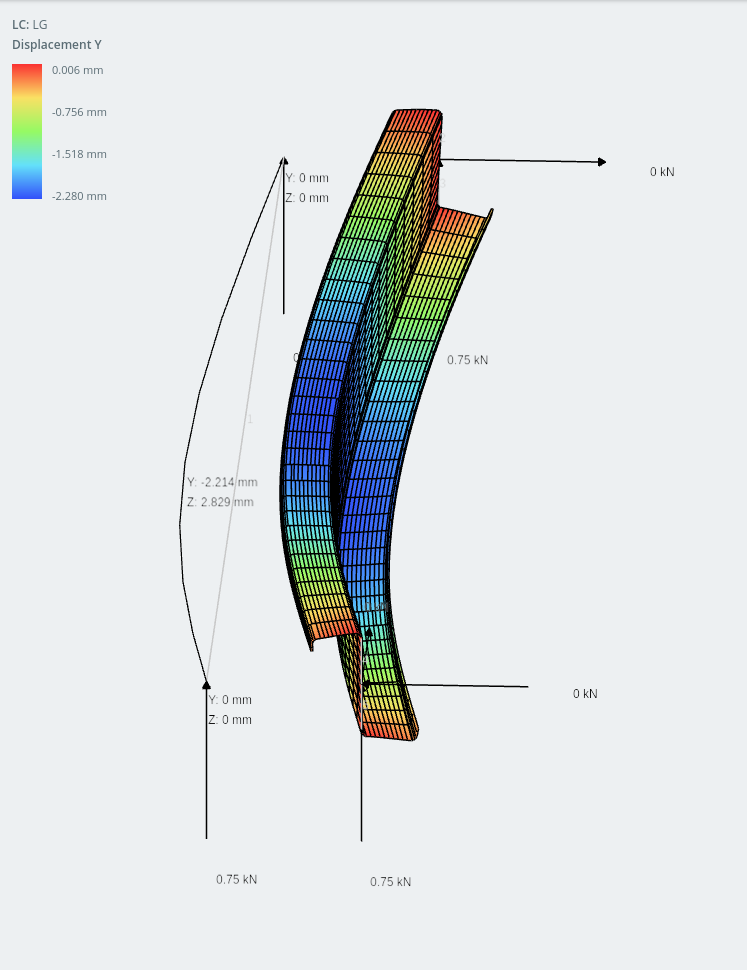
λιπ-ζ τμήμα (εμφανίζεται κάθετη μετατόπιση)

Τι είναι οι ασύμμετρες τομές. Τι είναι οι ασύμμετρες τομές?

Ελπίζω να βρήκατε αυτή την ανάρτηση ενδιαφέρουσα, εάν έχετε οποιεσδήποτε ερωτήσεις ή σχόλια σχετικά με τις ασύμμετρες ενότητες, ή θα θέλατε να δείτε περισσότερο περιεχόμενο όπως αυτό, αφήστε ένα σχόλιο παρακάτω.