Pデルタ効果とは?
もちろん, 構造モデルがロードされると変形します. 部材の端部の位置が変わっているため、たわみ構造は大きな二次モーメントに遭遇する可能性があります. これを説明するには, 以下に示す簡単な片持ち柱の例を考えてみましょう: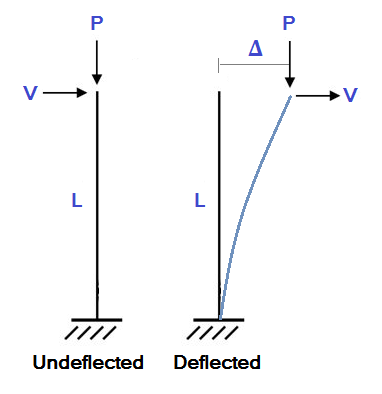
この例では, 長さLの柱が軸方向荷重に遭遇している (P) 横荷重 (V ). 標準線形静的解析では、横方向のたわみを計算します (Δ) なので:
[数学]
\デルタ= dfrac{ML ^ 2}{3番号} = dfrac{VL ^ 3}{3番号} \テキスト{ M = VLなので}
[数学]
線形静的解析の場合、横方向のたわみが, Δ, 横荷重による (V ). しかしながら, カラムが軸方向荷重に遭遇している場合 (P), その後、カラムはさらに偏向しません? 軸方向の荷重はP×Δの値を持つ二次モーメントを誘発するため、これは明らかです。. これを説明するには, 列のベースに関するモーメントを合計しましょう:
[数学]
\和{M}=(V times L) + (P times Delta)= VL + P Delta \\\\
M_{1} = VL \\\\
M_{2} = P Delta
[数学]
ここM1 横方向の点荷重が原因です, M2 アキシアル荷重による. これらの各モーメントは、横方向のたわみに異なる形で寄与します (点荷重とモーメントによる端部たわみのカンチレバー式を調べることができます, これらの式のそれぞれ):
[数学]
\デルタ_{1} = dfrac{M_{1}L ^ 2}{3番号} = dfrac{VL ^ 3}{3番号} \\\\
\デルタ_{2} = dfrac{M_{2}L ^ 2}{2番号} = dfrac{P Delta L ^ 2}{2番号}
[数学]
本当に, 横方向の総たわみは:
[数学]
\デルタ_{新着} = Delta_{1} + \デルタ_{2} = dfrac{VL ^ 3}{3番号} + \dfrac{P Delta L ^ 2}{2番号}
[数学]
元のたわみ値と比較すると、, PとΔに関して右側に追加の項があります. PまたはΔが有意な値である場合, 標準の線形静解析では、柱のたわみが過小評価されます. P-Delta Analysisは二次モーメントにちなんで名付けられていることは明らかです。 PD. したがって, Pデルタ効果は、幾何学的な非線形性によって引き起こされます. このために, P-Delta Analysisはしばしば 非線形分析. 適切なPデルタ分析は、Δの値を更新するために上記のプロセスを繰り返し続けます新着.
Pデルタ分析の実施について心配する必要があるのはいつですか?
良いニュースは SkyCiv構造3D P-Delta Analysisを実行できるようになりました. P-Delta効果は通常、風や他の力による重力負荷と横方向変位を経験している背の高い構造で流行します. 構造全体の横方向変位および/または垂直軸方向荷重が大きい場合, 非線形性を説明するためにPデルタ分析を実行する必要があります. 多くの場合, 線形静解析は 過小評価 変位 (他の結果の中で) Pデルタと比較して (非線形) 分析. P-Delta Non-Linear Analysisの重要性は、以下の例で説明されています. 建物の高層フレームは高さ20mです, 各階が5mの高さ. 柱はベースに完全に固定され、各レベルに負荷が分散されます. さらに, 最上階に垂直荷重があり、自重が考慮されるため、重力荷重をシミュレーションできます. もあります 比較的小さい 構造の側面に加えられた横方向の荷重.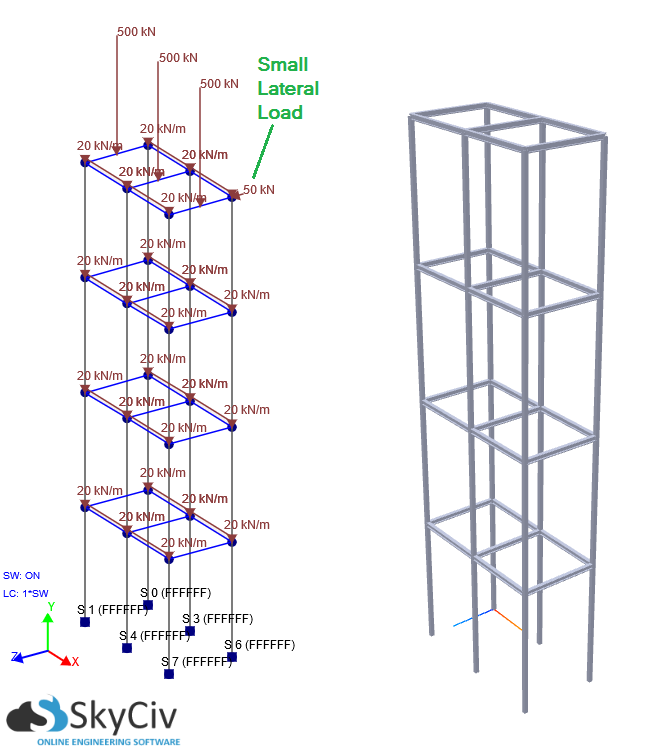
これらの条件下で、線形とPデルタの結果を比較してみましょう (非線形) 分析:
| 線形 | Pデルタ (非線形) | % 差 | |
|---|---|---|---|
| 最大総変位 | 254 んん | 353 んん | + 39% |
| 最大垂直反応 | 629 kN | 668 kN | + 6% |
| 最大モーメント反応 | 42 kN-m | 60 kN-m | + 43% |
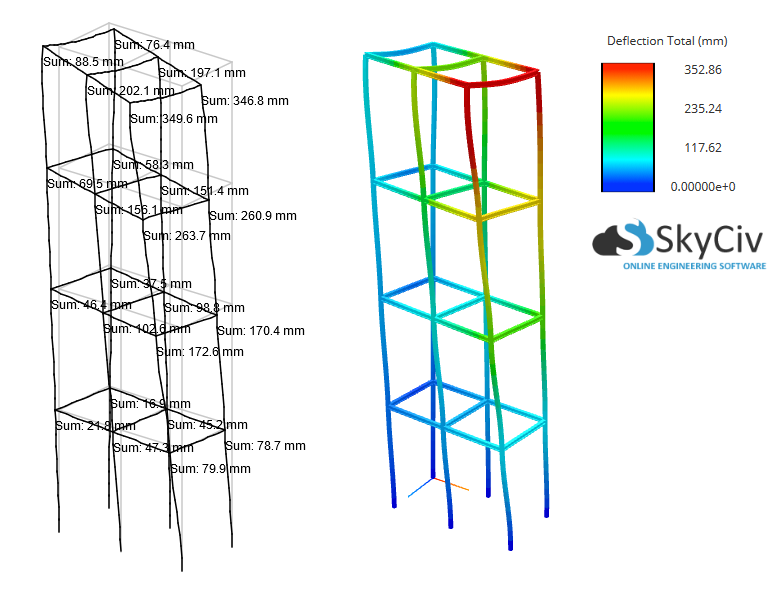P-Delta効果がこの構造で非常に重要な役割を果たすことは明らかです, 最大たわみと最大モーメントの結果を約 40%! したがって, このような場合、線形静解析は不十分です。.
要約すれば, P-Delta Analysisは、モデルの予期しない非線形性を考慮に入れるため、線形静解析よりも望ましい. 使用できます SkyCiv構造3D モデルで高速かつ効果的なP-Delta分析を実行する; 単に選択 "Pデルタ分析" クリックしたとき "解決する。" ソフトウェアがあなたのために仕事をしてくれるようにあなたが心配しなければならないすべてはデザインです!
ポールコミノ
CTOとSkyCivの共同創設者
機械式 (Hons1), BCom
LinkedIn
CTOとSkyCivの共同創設者
機械式 (Hons1), BCom
