O que é análise P-Delta? | SkyCiv Engenharia

A Análise P-Delta é um tipo de análise que é particularmente importante para o deslocamento lateral de estruturas de edifícios de vários andares que sofrem uma carga de gravidade. Neste artigo, SkyCiv Online Engineering Software irá discutir a teoria simples por trás dos efeitos P-Delta e ajudá-lo a entender a importância de tal análise ao modelar suas estruturas.

O que são efeitos P-Delta?

É claro, qualquer modelo estrutural irá desviar quando for carregado. Uma estrutura defletida pode encontrar momentos secundários significativos porque as extremidades dos membros mudaram de posição. Para ilustrar isso, considere o exemplo simples de coluna em balanço mostrado abaixo: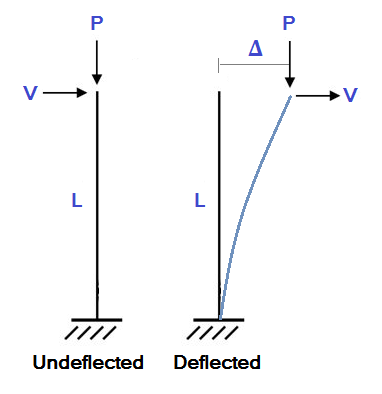

Neste exemplo, uma coluna de comprimento L está encontrando uma carga axial (P) e uma carga lateral (V). Em uma análise estática linear padrão, calcularíamos a deflexão lateral (Δ) como: [math] \Delta = dfrac{ML ^ 2}{3NÃO} = dfrac{VL ^ 3}{3NÃO} \texto{ já que M = VL} [math] Observe que, no caso de uma análise estática linear, a deflexão lateral, Δ, depende da carga lateral (V). Contudo, se a coluna está encontrando uma carga axial (P), então a coluna não desviaria ainda mais? Isso é óbvio porque a carga axial induziria um momento secundário com um valor de P × Δ. Para ilustrar isso, vamos somar os momentos sobre a base da coluna: [math] \soma{M}=(V times L) + (P times Delta)= VL + P Delta \\\\ M_{1} = VL \\\\ M_{2} = P Delta [math] Aqui M₁ é devido à carga do ponto lateral, enquanto, M₂ é devido à carga axial. Cada um desses momentos contribui para a deflexão lateral de forma diferente (você pode consultar as fórmulas do cantilever para a deflexão final devido a uma carga pontual e um momento, respectivamente para essas fórmulas): [math] \Delta_{1} = dfrac{M_{1}L ^ 2}{3NÃO} = dfrac{VL ^ 3}{3NÃO} \\\\ \Delta_{2} = dfrac{M_{2}L ^ 2}{2NÃO} = dfrac{P Delta L ^ 2}{2NÃO} [math] Então realmente, a deflexão lateral total seria mais próxima de: [math] \Delta_{novo} = Delta_{1} + \Delta_{2} = dfrac{VL ^ 3}{3NÃO} + \dfrac{P Delta L ^ 2}{2NÃO} [math] Podemos ver que, em comparação com o valor de deflexão original, há um termo extra à direita em termos de P e Δ. Se P ou Δ são valores significativos, a análise estática linear padrão estaria subestimando a deflexão da coluna. Deve ser óbvio agora que uma Análise P-Delta é nomeada após o momento secundário PD. Portanto, Os efeitos P-Delta são causados pela não linearidade geométrica. Por esta razão, uma análise P-Delta é muitas vezes chamada de Análise Não Linear. Uma análise P-Delta adequada continuaria a iterar o processo acima para atualizar o valor de Δ_novo.

Quando preciso me preocupar com a realização de uma análise P-Delta?

A boa notícia é que SkyCiv Structural 3D agora pode realizar uma análise P-Delta para você. Os efeitos P-Delta geralmente se tornam predominantes em estruturas altas que estão enfrentando cargas de gravidade e deslocamento lateral devido ao vento ou outras forças. Se o deslocamento lateral e / ou as cargas axiais verticais através da estrutura são significativas, uma análise P-Delta deve ser realizada para levar em conta as não linearidades. Em muitos casos, uma análise estática linear pode subestimar severamente deslocamento (entre outros resultados) em comparação com um P-Delta (Não Linear) Análise. A importância de uma análise não linear P-Delta será ilustrada no exemplo abaixo. A estrutura de vários andares do edifício tem 20 m de altura, com cada andar tendo 5 m de altura. As colunas são totalmente fixas na base com cargas distribuídas em cada nível. Além disso, existem cargas verticais no piso superior e o peso próprio é considerado para que as cargas de gravidade possam ser simuladas. Há também um relativamente pequeno carga lateral aplicada ao lado da estrutura.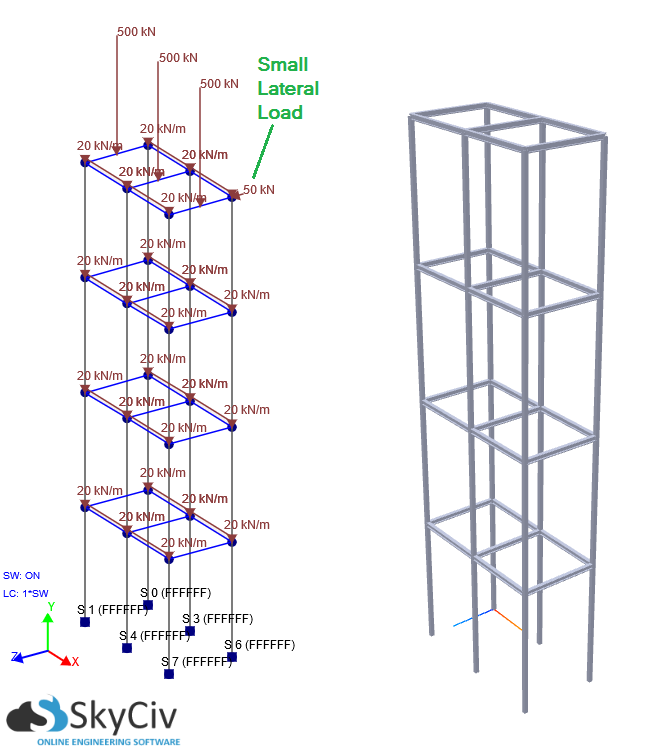

Sob essas condições, vamos comparar os resultados entre um Linear e um P-Delta (Não Linear) Análise:

	carga lineal	P-Delta (Não Linear)	% Diferença
Deslocamento Máx. Total	254 milímetros	353 milímetros	+ 39%
Reação vertical máxima	629 kN	668 kN	+ 6%
Reação de momento máximo	42 kN-m	60 kN-m	+ 43%

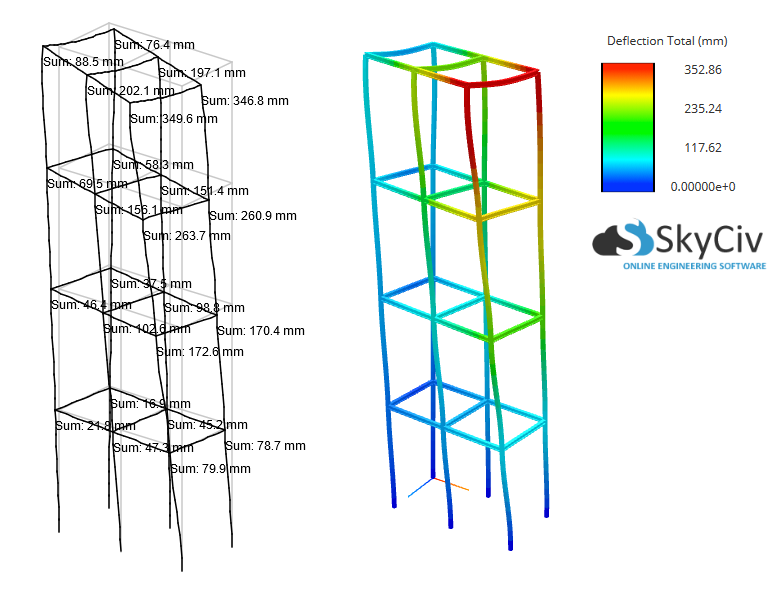É claro que os efeitos P-Delta desempenham um papel extremamente significativo com esta estrutura, aumentando os resultados de deflexão máxima e momento máximo em cerca de 40%! Por isso, uma análise estática linear é inadequada em tal caso. Resumindo, A análise P-Delta é preferível à análise estática linear, pois leva em consideração não linearidades imprevistas em seu modelo. Você pode usar SkyCiv Structural 3D para realizar análises P-Delta rápidas e eficazes em seus modelos; simplesmente selecione "Análise P-Delta" ao clicar "Resolver." Deixe o software fazer o trabalho por você, então tudo que você precisa se preocupar é o design!