Wat is P-Delta-analyse?

  P-Delta-analyse is een type analyse dat vooral belangrijk is voor het zijdelings verplaatsen van gebouwconstructies met meerdere verdiepingen die onder zwaartekracht staan. In dit artikel, SkyCiv online technische software bespreekt de eenvoudige theorie achter P-Delta-effecten en helpt u het belang van een dergelijke analyse te begrijpen bij het modelleren van uw structuren.  

Wat zijn P-Delta-effecten?

Natuurlijk, elk structureel model zal afbuigen wanneer het wordt geladen. Een afgebogen constructie kan aanzienlijke secundaire momenten tegenkomen omdat de uiteinden van de leden van positie zijn veranderd. Om dit te illustreren, overweeg het eenvoudige voorbeeld van een vrijdragende kolom hieronder: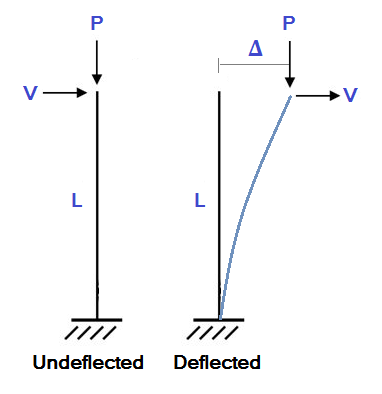 In dit voorbeeld, een kolom met lengte L ondervindt een axiale belasting (P.) en een zijdelingse belasting (V ). In een standaard lineaire statische analyse zouden we de laterale doorbuiging berekenen (Δ) net zo: [wiskunde] \Delta = dfrac{ML ^ 2}{3NEE} = dfrac{VL ^ 3}{3NEE} \tekst{ aangezien M = VL} [wiskunde] Merk op dat in het geval van een lineaire statische analyse de laterale doorbuiging, Δ, hangt af van de zijdelingse belasting (V ). Echter, als de kolom een ​​axiale belasting ondervindt (P.), dan zou de kolom niet nog meer afbuigen? Dit is duidelijk omdat de axiale belasting een secundair moment zou induceren met een waarde van P × Δ. Om dit te illustreren, laten we de momenten rond de basis van de kolom optellen: [wiskunde] \som{M}=(V maal L) + (P times Delta)= VL + P Delta \\\\ M_{1} = VL \\\\ M_{2} = P Delta [wiskunde] Hier M₁ is te wijten aan de laterale puntbelasting while, M₂ is te wijten aan de axiale belasting. Elk van deze momenten draagt ​​op een andere manier bij aan de laterale afbuiging (je kunt de cantilever-formules opzoeken voor de einddoorbuiging vanwege een puntbelasting en een moment, respectievelijk voor deze formules): [wiskunde] \Delta_{1} = dfrac{M_{1}L ^ 2}{3NEE} = dfrac{VL ^ 3}{3NEE} \\\\ \Delta_{2} = dfrac{M_{2}L ^ 2}{2NEE} = dfrac{P Delta L ^ 2}{2NEE} [wiskunde] Dus echt, de totale laterale afbuiging zou dichter bij zijn: [wiskunde] \Delta_{nieuw} = Delta_{1} + \Delta_{2} = dfrac{VL ^ 3}{3NEE} + \dfrac{P Delta L ^ 2}{2NEE} [wiskunde] We kunnen dat zien in vergelijking met de oorspronkelijke doorbuigingswaarde, rechts staat een extra term in termen van P en Δ. Als P of Δ significante waarden zijn, de standaard lineaire statische analyse zou de doorbuiging van de kolom onderschatten. Het mag nu duidelijk zijn dat een P-Delta Analyse vernoemd is naar het secundaire moment PD. Daarom, P-Delta-effecten worden veroorzaakt door geometrische niet-lineariteit. Om deze reden, een P-Delta-analyse wordt vaak een Niet-lineaire analyse. Een juiste P-Delta-analyse zou het bovenstaande proces blijven herhalen om de waarde van Δ bij te werken_nieuw.

Wanneer moet ik me zorgen maken over het uitvoeren van een P-Delta-analyse?

Het goede nieuws is dat SkyCiv Structural 3D kan nu een P-Delta-analyse voor u uitvoeren. P-Delta-effecten komen meestal voor in hoge constructies die onderhevig zijn aan zwaartekrachtbelastingen en laterale verplaatsing als gevolg van wind of andere krachten. Als de laterale verplaatsing en / of de verticale axiale belastingen door de constructie significant zijn, een P-Delta-analyse moet worden uitgevoerd om rekening te houden met de niet-lineariteiten. Vaak, een lineaire statische analyse kan ernstig onderschat verplaatsing (onder andere resultaten) in vergelijking met een P-Delta (Niet-lineair) Analyse. Het belang van een P-Delta niet-lineaire analyse wordt geïllustreerd in het onderstaande voorbeeld. Het frame van het gebouw met meerdere verdiepingen is 20 meter hoog, waarbij elke verdieping 5 meter hoog is. De kolommen zijn volledig bevestigd aan de basis met verdeelde belastingen op elk niveau. Bovendien, er zijn verticale belastingen op de bovenste verdieping en er wordt rekening gehouden met het eigen gewicht, zodat zwaartekrachtbelastingen kunnen worden gesimuleerd. Er is ook een relatief klein zijdelingse belasting uitgeoefend op de zijkant van de constructie.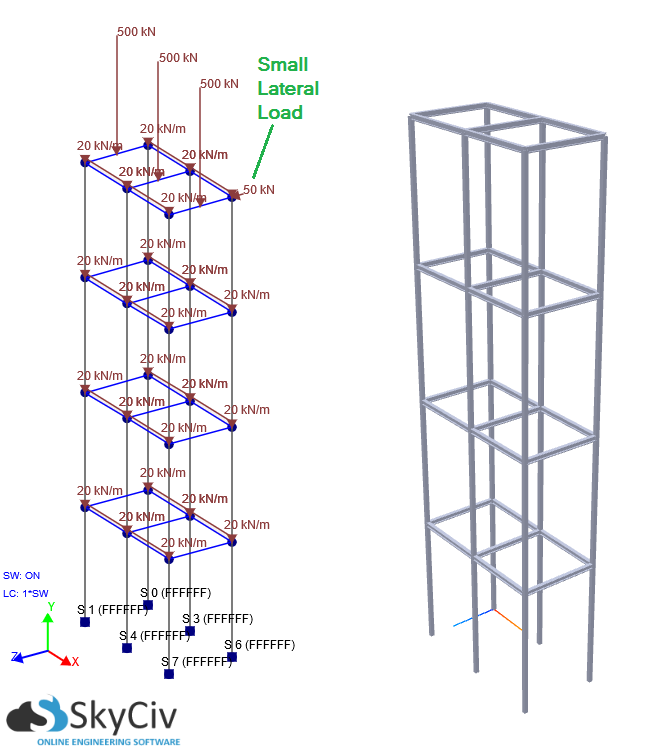   Laten we onder deze omstandigheden de resultaten tussen een lineaire en een P-delta vergelijken (Niet-lineair) Analyse:

	Lineair	P-Delta (Niet-lineair)	% Verschil
Max. Totale verplaatsing	254 mm	353 mm	+ 39%
Maximale verticale reactie	629 kN	668 kN	+ 6%
Max Moment Reactie	42 kN-m	60 kN-m	+ 43%

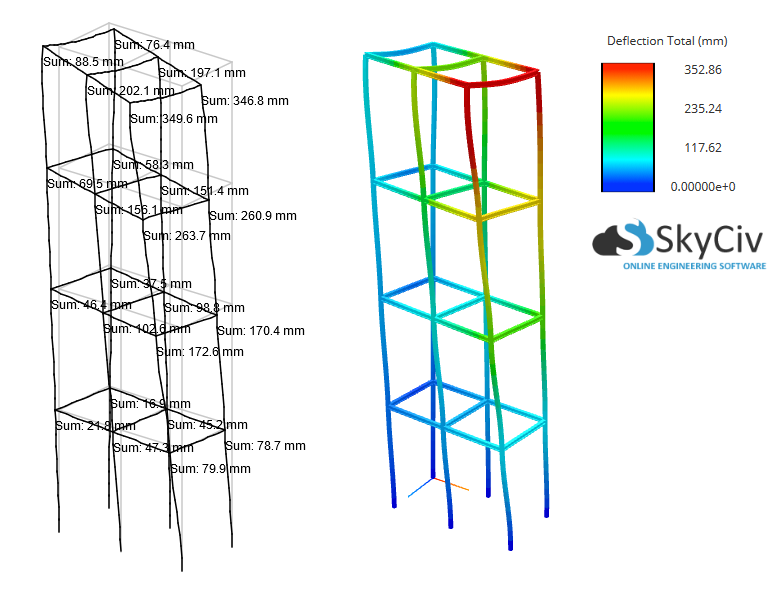Het is duidelijk dat P-Delta-effecten een zeer belangrijke rol spelen bij deze structuur, het verhogen van de maximale doorbuiging en het maximale moment resulteert met ongeveer 40%! Dus, een lineaire statische analyse is in zo'n geval niet toereikend. samengevat, P-Delta-analyse heeft de voorkeur boven lineaire statische analyse, omdat deze rekening houdt met onvoorziene niet-lineariteiten in uw model. Je kunt gebruiken SkyCiv Structural 3D om snelle en effectieve P-Delta-analyses op uw modellen uit te voeren; gewoon selecteren "P-Delta-analyse" bij het klikken "Oplossen." Laat de software het werk voor u doen, dus u hoeft zich alleen maar zorgen te maken over het ontwerp!  

Gratis inschrijven