Στο SkyCiv πιστεύουμε ότι η εκπαίδευση είναι σημαντική, οπότε δεσμευόμαστε να βοηθήσουμε την επόμενη γενιά μηχανικών να μάθει τη δομική μηχανική. Στο πλαίσιο αυτής της αποστολής, αναπτύσσουμε Αναφορές υπολογισμού χειρός μεθόδου διανομής στιγμών που ανοίγουν το μαύρο κουτί του λογισμικού δομικής μηχανικής, εκθέτοντάς τα στα περίεργα μυαλά των χρηστών μας. Οι μηχανικοί θέλουν να γνωρίζουν πώς και γιατί κάτι είναι έτσι, και συχνά ο καλύτερος τρόπος για να το μάθετε αυτό είναι να προσπαθήσετε να το επιλύσετε μόνοι σας και να συγκρίνετε τη λύση σας με μια λύση που είναι πλήρης και σωστή. Εξισορροπούν την αναγνωσιμότητα των αναφορών μας με το επίπεδο λεπτομέρειας που απαιτείται για τον έλεγχο των υπολογισμών, βήμα βήμα. Αυτό είναι θεμελιώδες για την πρακτική της μηχανικής και θα συνεχίσουμε να παρέχουμε στους χρήστες εργαλεία που προσθέτουν αξία στην εκπαίδευσή τους, εργασία, και ζει.
Είμαστε καθοδηγημένοι από αυτό που θέλετε: Ένα από τα πιο απαιτούμενα χαρακτηριστικά από τους χρήστες μας ήταν οι υπολογισμοί χεριών για απροσδιόριστα δοκάρια. Είμαστε περήφανοι που ανακοινώνουμε ότι αυτή η λειτουργία είναι πλέον ζωντανή: Τωρινός μαθητής, Οι βασικοί και επαγγελματίες χρήστες μπορούν Δοκίμασέ το τώρα. Για απροσδιόριστες δοκούς χωρίς μεντεσέδες, οι κατακόρυφες και στιγμιαίες αντιδράσεις επιλύονται χρησιμοποιώντας τη μέθοδο κατανομής ροπής.
Η ενότητα Υπολογισμός Χειρός Μέθοδος Κατανομής Ροπών, θα δείξει εύκολα τους υπολογισμούς χεριών για μια ακτίνα όπως τα ακόλουθα:
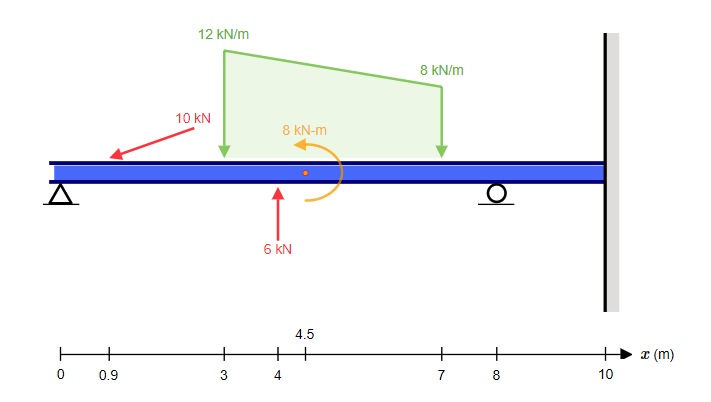
Οι υπάρχοντες χρήστες θα είναι εξοικειωμένοι με την πρόσβαση σε υπολογισμούς χεριών για στατιστικά καθορισμένες δομές στο Beam, ωστόσο, εάν είστε νέοι στο SkyCiv ή δεν έχετε δοκιμάσει ακόμη υπολογισμούς χεριών, μας τεκμηρίωση μπορεί να σας καθοδηγήσει στη διαδικασία.
Μέθοδος κατανομής στιγμής
Μέθοδος κατανομής στιγμής (MDM), εφευρέθηκε από τον Hardy Cross, είναι εξαιρετικά ισχυρό στην απλότητά του και έχει χρησιμοποιηθεί εκτενώς από την πρώτη του έκδοση από το περιοδικό ASCE το 1930. Μέρος της απλότητάς του έγκειται στον τρόπο με τον οποίο το διάγραμμα ροπής κάμψης μπορεί να σχεδιαστεί γραφικά χρησιμοποιώντας την υπέρθεση χωρίς να χρειάζεται να υπολογίσετε τις εξισώσεις ασυνέχειας για κάθε τμήμα. Οι σύνθετες δομές μπορούν να λυθούν σχετικά εύκολα σε σύγκριση με άλλες μεθόδους όπως η FEM, τη μέθοδο εικονικής μετατόπισης, ή επίλυση εξισώσεων ασυνέχειας. Το MDM μπορεί να χρησιμοποιηθεί σε μια ποικιλία δομών 2D όπως δοκάρια και πλαίσια.
Ο Hardy Cross ήταν δομικός μηχανικός σε μια περίοδο κατά την οποία ο υπολογισμός των χεριών ήταν απαραίτητη άσκηση για κάθε δομικό μηχανικό. Μετά την επανάληψη της διαδικασίας υπολογισμού των δομών αμέτρητες φορές αναγνώρισε ότι ουσιαστικά ολοκλήρωσε τους ίδιους υπολογισμούς ξανά και ξανά. Αυτό οδήγησε τον Σταυρό να διερευνήσει μια θεωρία ότι οι σύνθετες δομές ήταν πραγματικά συνδυασμοί απλών δομών και, Αυτές οι απλές δομές θα μπορούσαν να συναρμολογηθούν για να δημιουργήσουν τη σύνθετη δομή με την ίδια αναλυτική λύση. Οι απλές δομές είναι εύκολο να λυθούν, οι τύποι ήταν αρκετά εύκολο να προκύψουν ακόμη και αν ήταν απροσδιόριστοι, χάρη στην υπέρθεση και τη μέθοδο Virtual Force. Ο Cross δημιούργησε πίνακες αυτών των απλών δομών και προσπάθησε να δοκιμάσει τη θεωρία του με διάφορους τρόπους.
Εξισώσεις Στιγμιαίας Λήξης
Η μέθοδος κατανομής στιγμής χρησιμοποιεί πίνακες κοινών περιπτώσεων φόρτωσης για να αναζητήσει τις εξισώσεις για τις στιγμές στα άκρα κάθε τμήματος. Αυτοί οι πίνακες βρίσκονται στην τεκμηρίωσή μας για υπολογισμός διαγραμμάτων ροπής κάμψης και όχι μόνο αποτελούν τη βάση στην οποία χρησιμοποιείται το MDM, αλλά είναι επίσης μια εξαιρετική αναφορά για απλούς υπολογισμούς ροπής κάμψης. Ένας απλός τρόπος για να το δούμε είναι, το MDM διασπά τη δέσμη σε τμήματα, και χρησιμοποιεί αυτές τις απλές εξισώσεις για τον υπολογισμό του BMD.
Εναλλακτικές μέθοδοι
Ο υπολογισμός του διαγράμματος ροπής κάμψης μπορεί να επιτευχθεί με άλλους τρόπους, όπως η χρήση ασυνεχών εξισώσεων για τις οποίες έχουμε γράψει προηγουμένως εδώ.
Δείγμα αναφοράς



