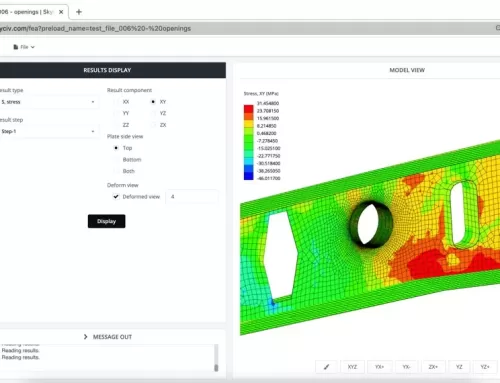
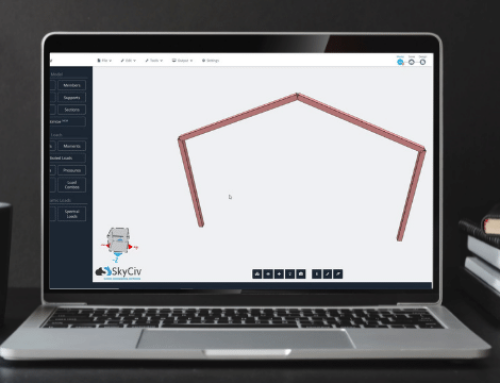
Secciones asimétricas
Las secciones asimétricas no son simétricas en el eje y vertical ni en el eje z horizontal o, en algunos casos, cualquier eje. Ejemplos de secciones asimétricas son ángulos y secciones en Z.
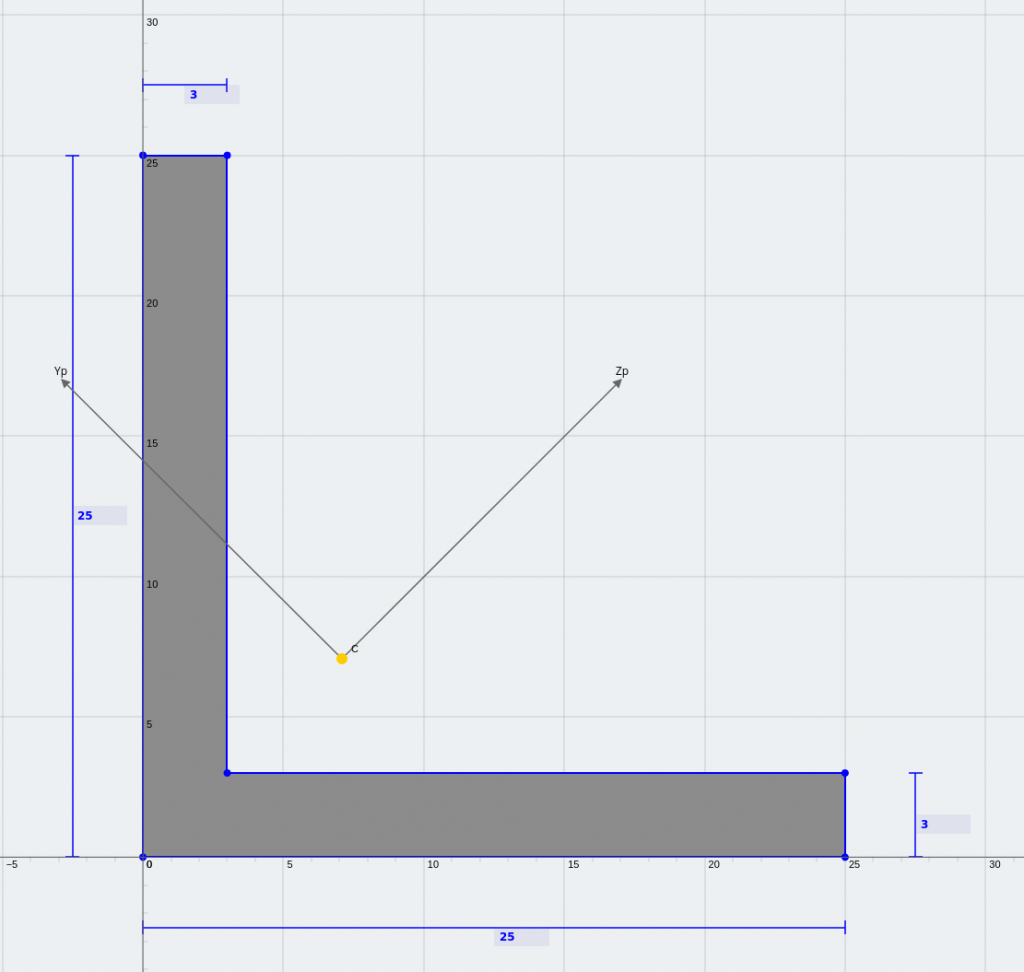
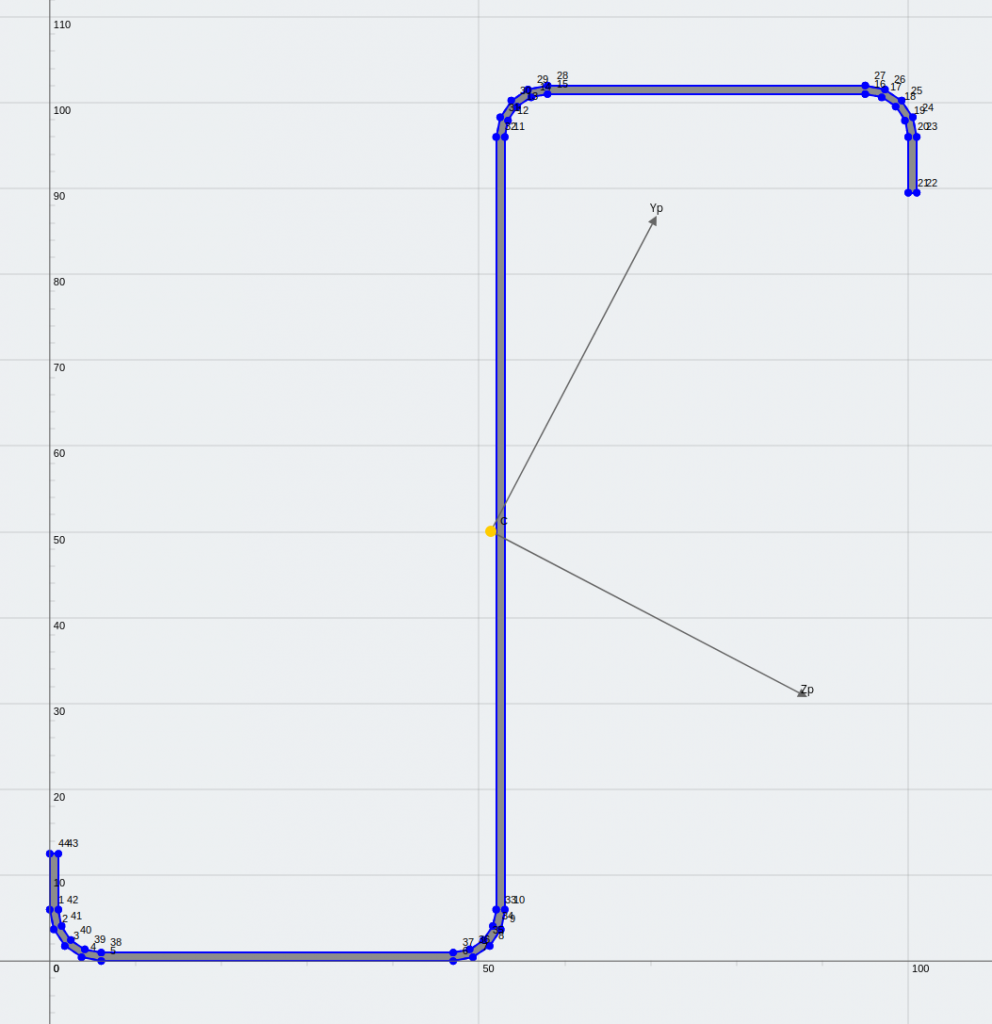
Una sección de ángulo igual (Una sección de ángulo igual)
Las vigas con secciones asimétricas se comportan de manera diferente a las vigas con bi-simetría en flexión. Incluso si la viga tiene una rigidez equivalente en el eje vertical, no se comportará como un RHS y la forma I sí lo hace..
En este ejemplo, demostraré su comportamiento con un caso de carga simple.: una carga vertical distribuida uniformemente.
3D
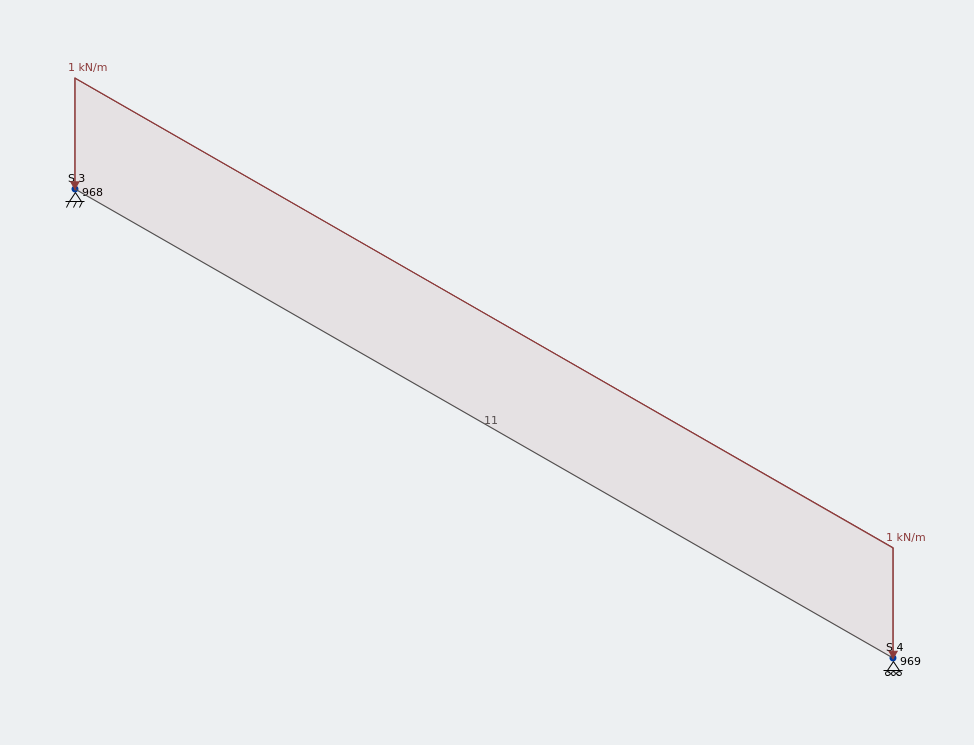
Modelo de marco de un 1.5 m ángulo igual bajo UDL vertical
He aplicado una carga distribuida uniformemente de 1 kN / m a lo largo de todo este 1.5 m ángulo igual.
Si quisiera comprobar la deflexión en la mitad del tramo de esta viga, podría fácilmente. Todo lo que necesitaría sería el segundo momento de área, y la fórmula de deflexión máxima estándar para vigas simplemente apoyadas. Un cálculo rápido usando SkyCiv Section Builder y obtengo las propiedades de la sección fácilmente.
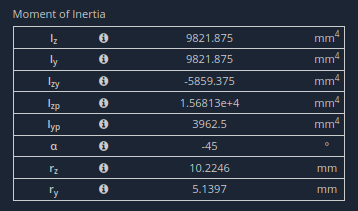
Propiedades de sección tabulada de SkyCiv Section Builder
Iz es 9821.9 mm a la 4ta potencia. La sección es de acero estructural con E = 200 GPa.

Mire lo que sucede cuando calculo esto con FEA en SkyCiv Structural 3D.
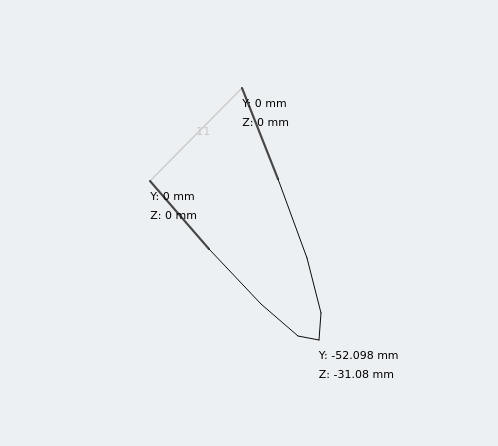
Desplazamiento de igual ángulo bajo carga
La sección de ángulo igual tiene dos componentes de deflexión! Analizando la deflexión de una viga simplemente apoyada usando una sección bi-simétrica usando el cálculo anterior, este sería un enfoque perfectamente aceptable para una verificación rápida.. Pero para las secciones asimétricas, necesitamos otra información..
El ángulo α
Tenga en cuenta que en las propiedades de la sección anterior, el valor de α es distinto de cero.
Esto significa que el eje principal no es paralelo a uno de los ejes geométricos..
Demostrar el efecto de rotar el eje en los valores de rigidez calculados., Dibujé debajo de la rigidez en los ejes horizontal y vertical a medida que se gira el sistema de coordenadas.
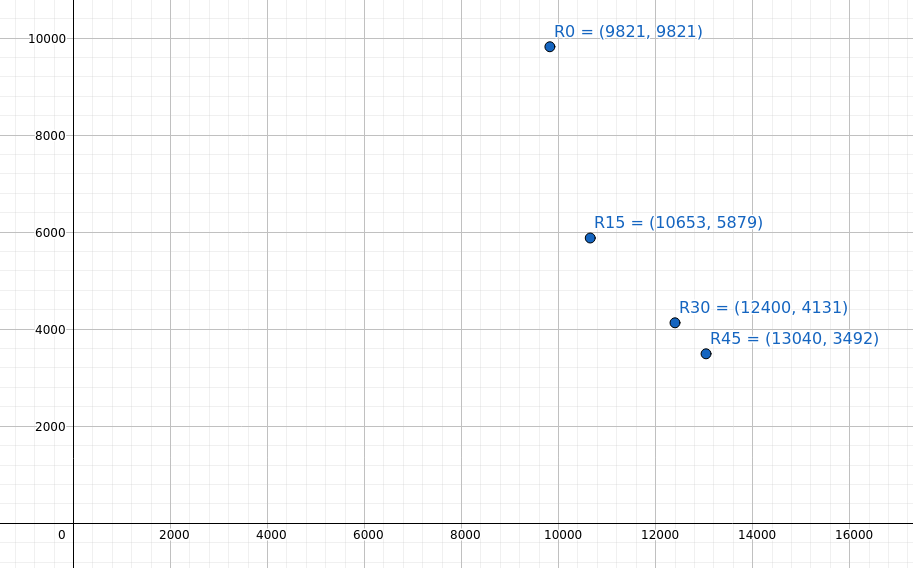
Rigidez de 25x25x3 EA después de rotar el sistema de coordenadas
Tenga en cuenta la curva no lineal que se está formando a medida que el sistema de coordenadas gira a través de 15, 30 y 45 grados. Esta curva será única para la sección..
Entonces, ¿por qué está pasando esto??
Un profesor me dijo una vez que las cargas siguen las partes más rígidas de la estructura.. En este caso, la carga está siendo transportada por el eje más rígido (el eje principal principal).
El enfoque correcto
La forma correcta de calcular los resultados de la deflexión implica transformar primero todas las cargas en los ejes principales, luego calculando las deflexiones basadas en el segundo momento de área a lo largo de los ejes principales. Para demostrar que este es de hecho el enfoque correcto, he validado la respuesta utilizando un cálculo manual., y para hacer esto un poco más interesante, con un modelo de la viga utilizando un elemento de marco y, un modelo construido a partir de conchas. De esa manera, no puede haber duda de que los desplazamientos que vimos antes son realmente correctos..
Aquí está el modelo que creé.
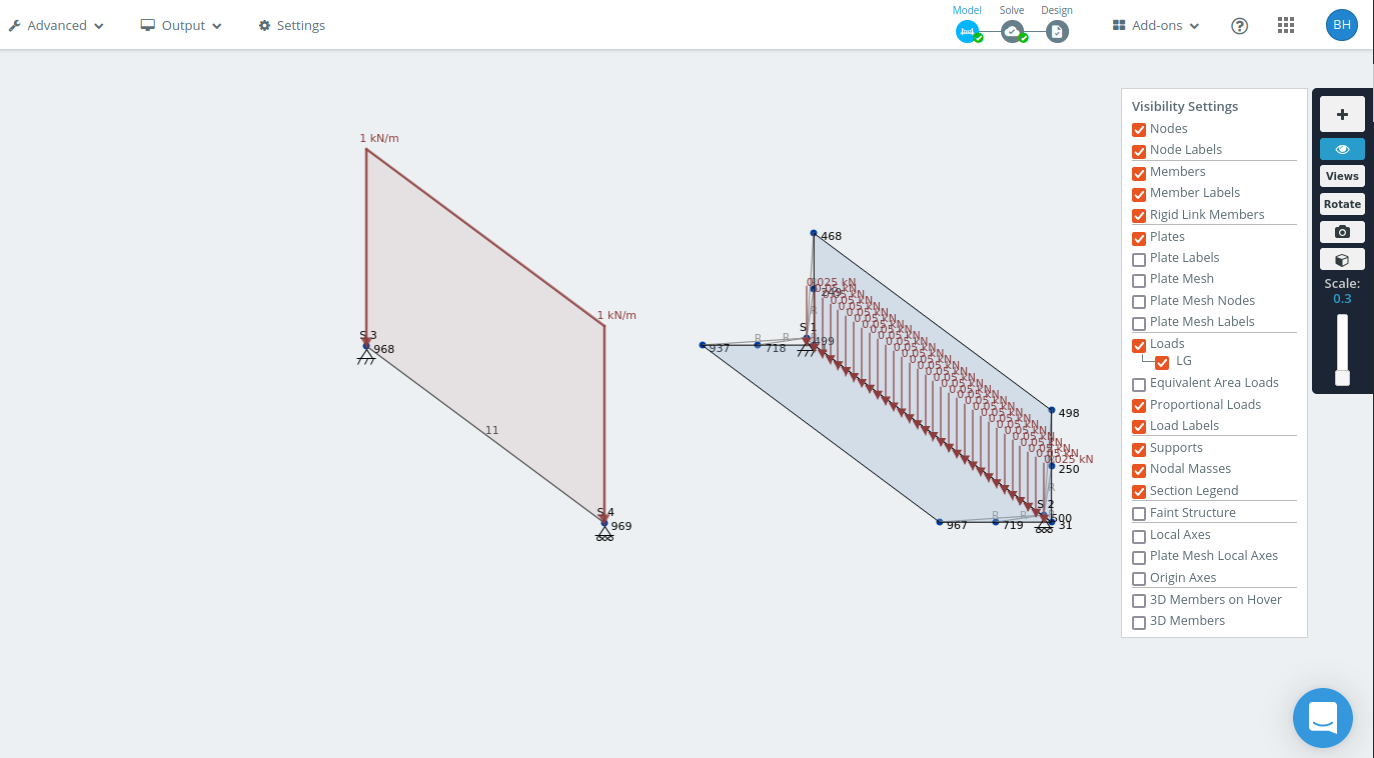
Modelo de estructura y modelo de carcasa de 1.5 ángulo m
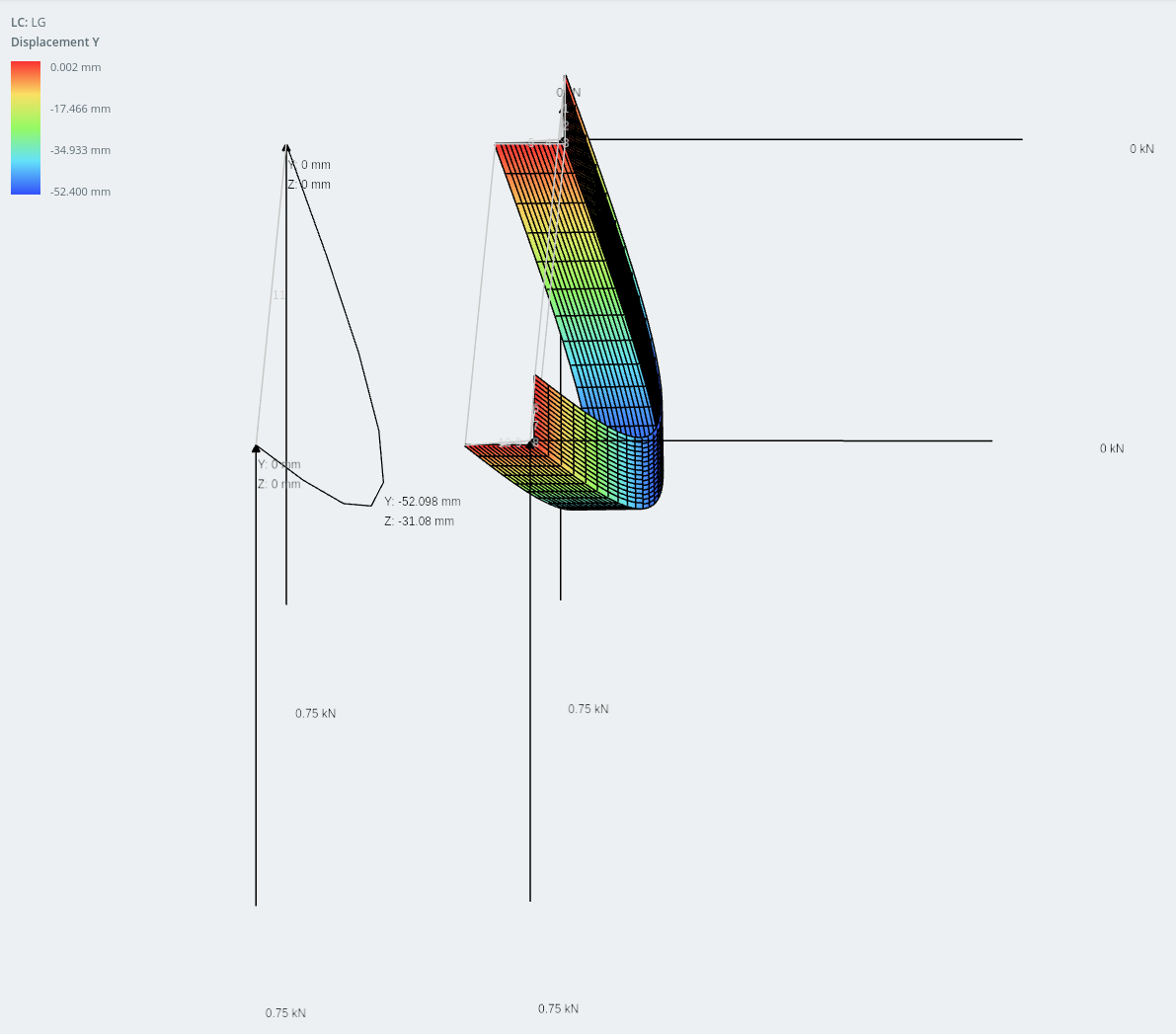
Desplazamiento en dirección vertical
La diferencia de resultados entre los dos modelos es extremadamente cercana: dentro 1% el uno del otro.
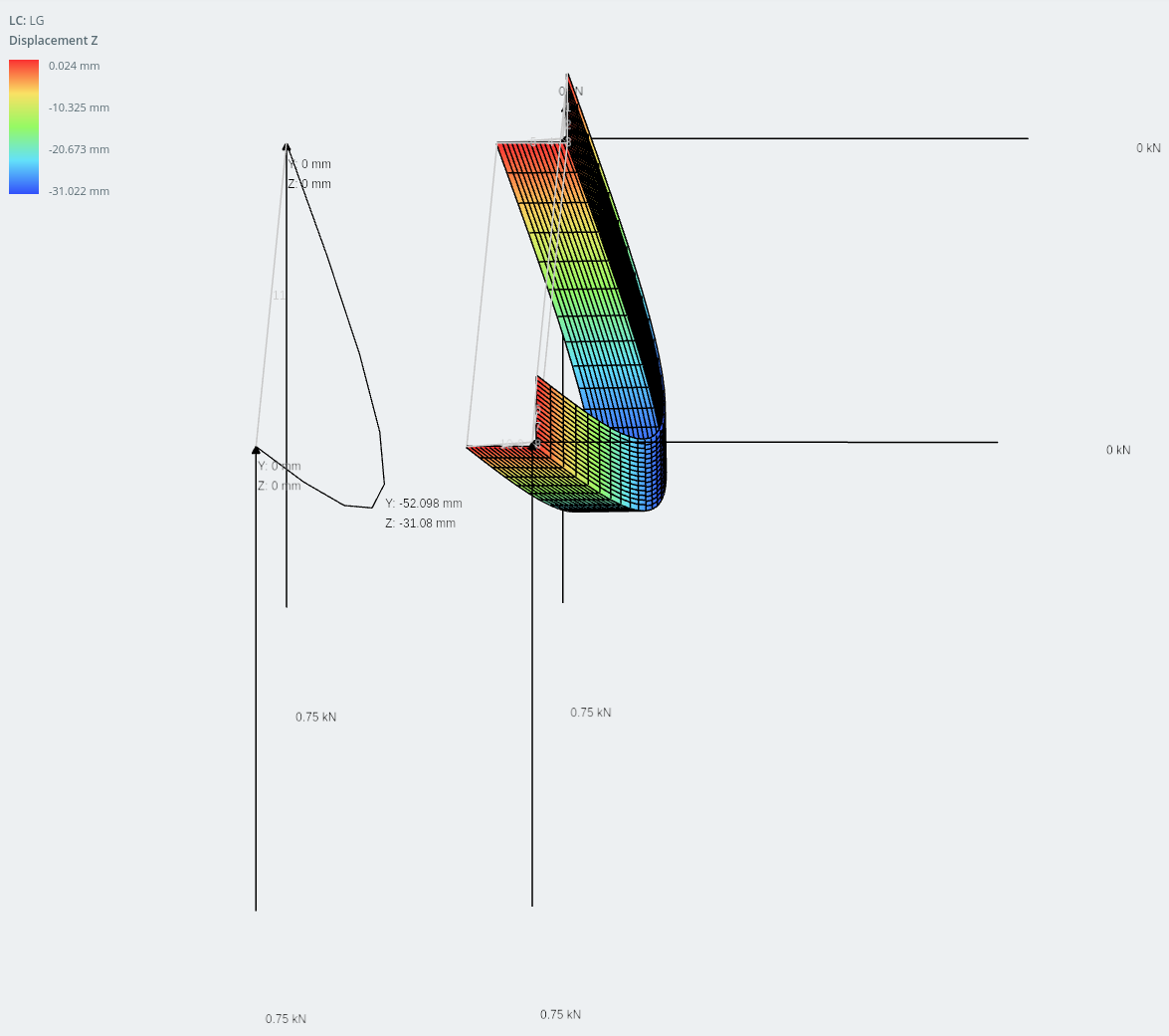
Desplazamiento en dirección horizontal.
Y están confirmados por los cálculos manuales a continuación..

Por qué querría utilizar estas secciones?
A los ingenieros les gusta diseñar estructuras que sean ligeras y eficientes, Sin embargo, a veces existen limitaciones en la forma de los componentes estructurales., normalmente debido a decisiones de diseño de otros. Esta restricción en la forma podría deberse a muchas razones, puede ser porque un arquitecto quiere ocultar elementos estructurales por razones estéticas, o para cumplir con las leyes de planificación locales. Puede ser que existan limitaciones debido a la capacidad de fabricación local o simplemente a la disponibilidad y el costo de las materias primas.. Los costos de fabricación y el revestimiento también pueden desempeñar un papel importante.. Algunas veces, estamos atrapados con lo que tenemos.
Cuando hay una eleccion, la sección se puede elegir porque tiene ciertas ventajas. Tomemos, por ejemplo, secciones Z, que se ven comúnmente soportando chapas de acero perfiladas inclinadas. Típicamente para pequeños ángulos de techo inclinados, Los canales son más eficientes porque las cargas de gravedad solo causan pequeños momentos alrededor del eje débil.. Estos momentos aumentan a medida que aumenta la inclinación del techo y con una cierta inclinación., Las secciones Z se vuelven más eficientes.
Para demostrar, modelé la sección en Z con reborde como una viga de acero de 1,5 m. Una sección de ángulo igual.
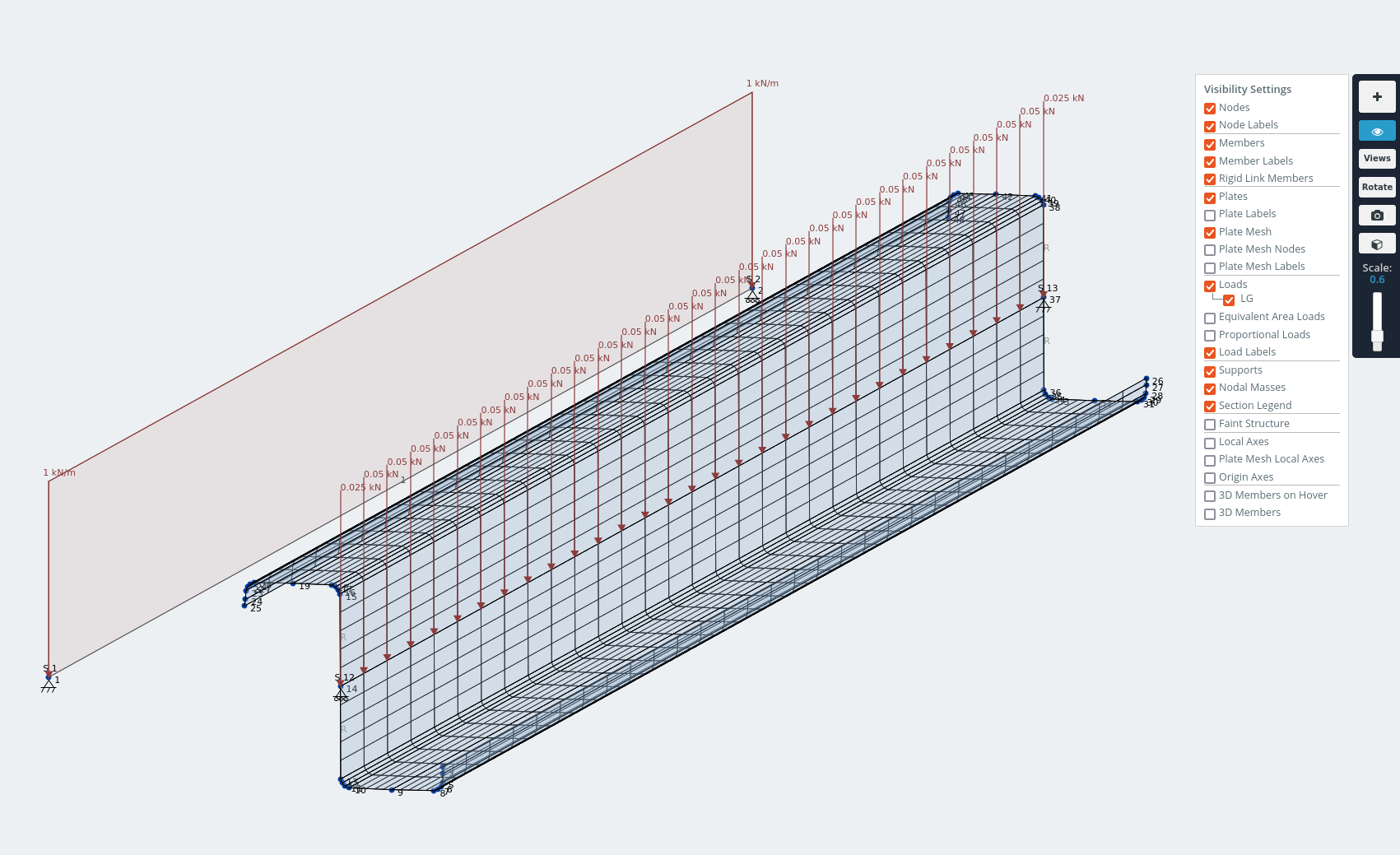
Modelo de sección en Z con reborde con carga distribuida de 1 kN / m aplicada a través del centro de corte.
El desplazamiento en el eje z se opone a la acción de corte en el plano de las láminas del techo bajo cargas de gravedad..
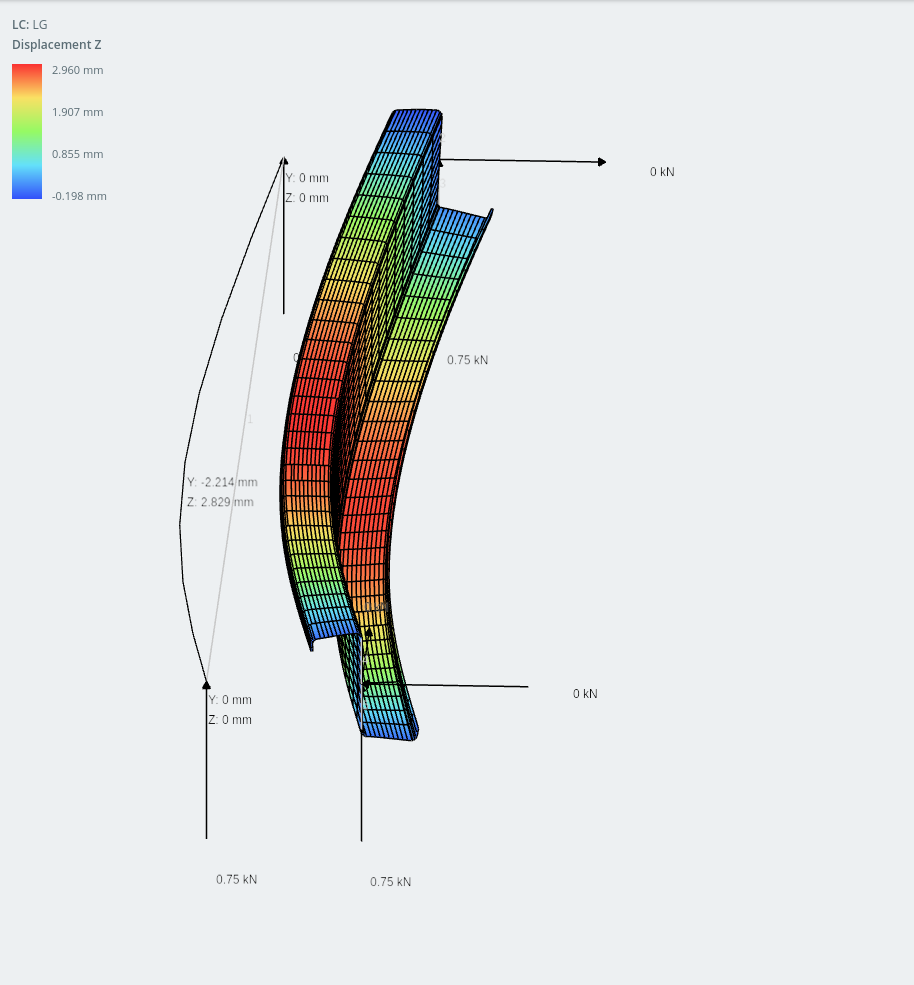
modelo de marco de sección en Z con labios y modelo de carcasa (desplazamiento horizontal mostrado en placas)
Asombrosamente, el desplazamiento en el eje y (vertical) es en realidad menor que en la horizontal. Una sección de ángulo igual, Una sección de ángulo igual, Una sección de ángulo igual, Una sección de ángulo igual!
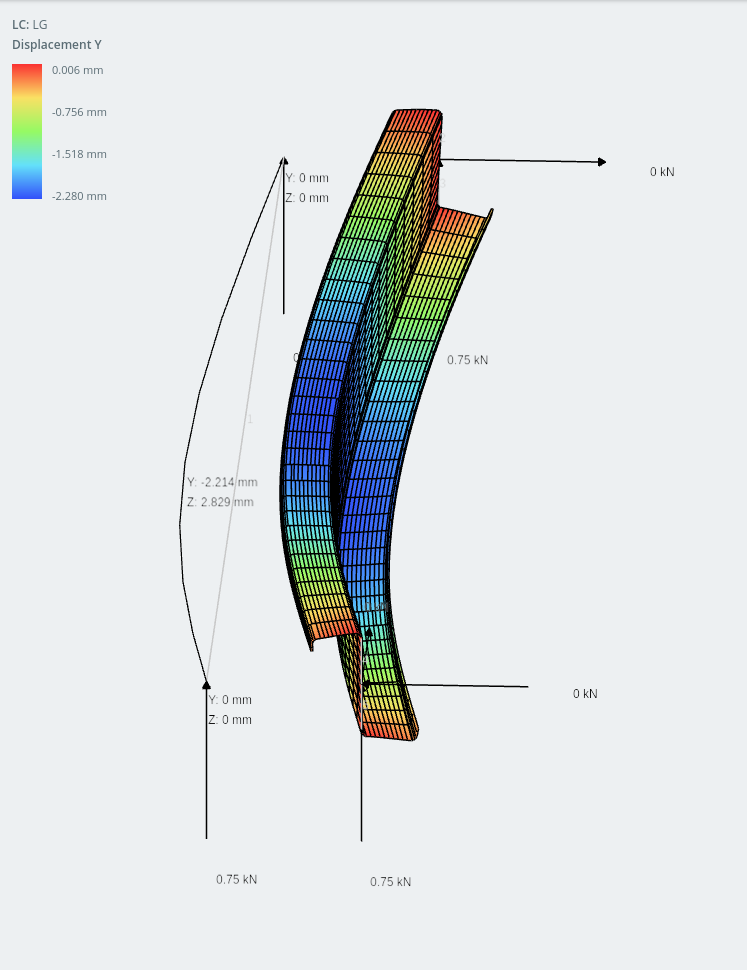
sección de labios en Z (se muestra el desplazamiento vertical)
Una sección de ángulo igual. Una sección de ángulo igual?
Espero que hayas encontrado interesante esta publicación., si tiene alguna pregunta o comentario sobre las secciones asimétricas, o le gustaría ver más contenido como este, deje un comentario a continuación.