¿Qué es el análisis P-Delta??

El análisis P-Delta es un tipo de análisis que es particularmente importante para el desplazamiento lateral de estructuras de edificios de varios pisos que experimentan una carga de gravedad. En este artículo, Software de ingeniería en línea SkyCiv discutirá la teoría simple detrás de los efectos P-Delta y lo ayudará a comprender la importancia de dicho análisis al modelar sus estructuras.

¿Qué son los efectos P-Delta??

Por supuesto, cualquier modelo estructural se desviará cuando se cargue. Una estructura desviada puede encontrar momentos secundarios significativos porque los extremos de los miembros han cambiado de posición.. Para ilustrar esto, considere el ejemplo de columna en voladizo simple que se muestra a continuación: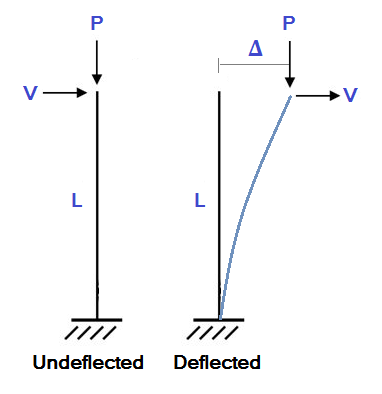

En este ejemplo, una columna de longitud L encuentra una carga axial (PAG) y una carga lateral (V ). En un análisis estático lineal estándar, calcularíamos la desviación lateral (Δ) como: [math] \Delta = dfrac{ML ^ 2}{3EI} = dfrac{VL ^ 3}{3EI} \texto{ ya que M = VL} [math] Observe que en el caso de un análisis estático lineal, la desviación lateral, Δ, depende de la carga lateral (V ). sin embargo, si la columna encuentra una carga axial (PAG), entonces la columna no se desviaría aún más? Esto es obvio porque la carga axial induciría un momento secundario con un valor de P × Δ. Para ilustrar esto, vamos a resumir los momentos sobre la base de la columna: [math] \suma{M}=(V veces L) + (P veces Delta)= VL + P Delta \\\\ METRO_{1} = VL \\\\ METRO_{2} = P Delta [math] Aquí m₁ se debe a la carga puntual lateral mientras que, M₂ se debe a la carga axial. Cada uno de estos momentos contribuye a la desviación lateral de manera diferente (puede buscar las fórmulas en voladizo para la desviación final debido a una carga puntual y un momento, respectivamente para estas fórmulas): [math] \Delta_{1} = dfrac{METRO_{1}L ^ 2}{3EI} = dfrac{VL ^ 3}{3EI} \\\\ \Delta_{2} = dfrac{METRO_{2}L ^ 2}{2EI} = dfrac{P Delta L ^ 2}{2EI} [math] Realmente, la desviación lateral total estaría más cerca de: [math] \Delta_{nuevo} = Delta_{1} + \Delta_{2} = dfrac{VL ^ 3}{3EI} + \dfrac{P Delta L ^ 2}{2EI} [math] Podemos ver eso en comparación con el valor de deflexión original, hay un término adicional a la derecha en términos de P y Δ. Si P o Δ son valores significativos, el análisis estático lineal estándar estaría subestimando la desviación de la columna. Debería ser obvio ahora que un análisis P-Delta lleva el nombre del momento secundario PD. Por lo tanto, Los efectos de P-Delta son causados por la no linealidad geométrica. Por esta razón, un análisis P-Delta a menudo se llama Análisis no lineal. Un análisis P-Delta adecuado continuaría iterando el proceso anterior para actualizar el valor de Δ_nuevo.

¿Cuándo debo preocuparme por realizar un análisis P-Delta??

La buena noticia es que SkyCiv Structural 3D ahora puede realizar un análisis P-Delta por usted. Los efectos de P-Delta generalmente se vuelven frecuentes en estructuras altas que experimentan cargas de gravedad y desplazamiento lateral debido al viento u otras fuerzas. Si el desplazamiento lateral y / o las cargas axiales verticales a través de la estructura son significativas, Se debe realizar un análisis P-Delta para tener en cuenta las no linealidades. En muchos casos, un análisis lineal estático puede subestimar severamente desplazamiento (entre otros resultados) en comparación con un P-Delta (No lineal) 3D. La importancia de un análisis no lineal P-Delta se ilustrará en el siguiente ejemplo. El marco de varios pisos del edificio tiene 20 m de altura, con cada piso de 5 m de altura. Las columnas están completamente fijas en la base con cargas distribuidas en cada nivel.. Adicionalmente, hay cargas verticales en el piso superior y se considera el peso propio, por lo que se pueden simular cargas de gravedad. También hay una relativamente pequeño carga lateral aplicada al costado de la estructura.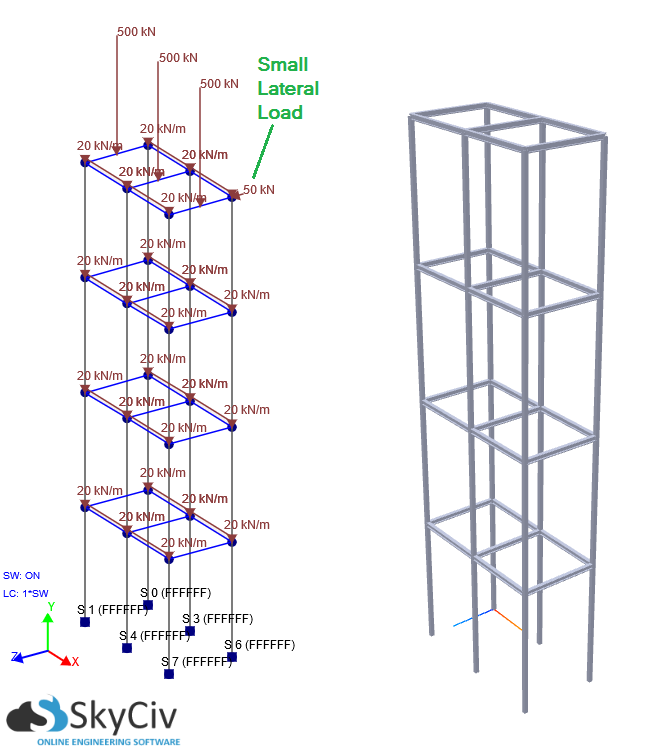

En estas condiciones, comparemos los resultados entre un lineal y un P-Delta (No lineal) 3D:

	Lineal	P-Delta (No lineal)	% Diferencia
Desplazamiento total máximo	254 mm	353 mm	+ 39%
Reacción vertical máxima	629 kN	668 kN	+ 6%
Reacción de momento máximo	42 kN-m	60 kN-m	+ 43%

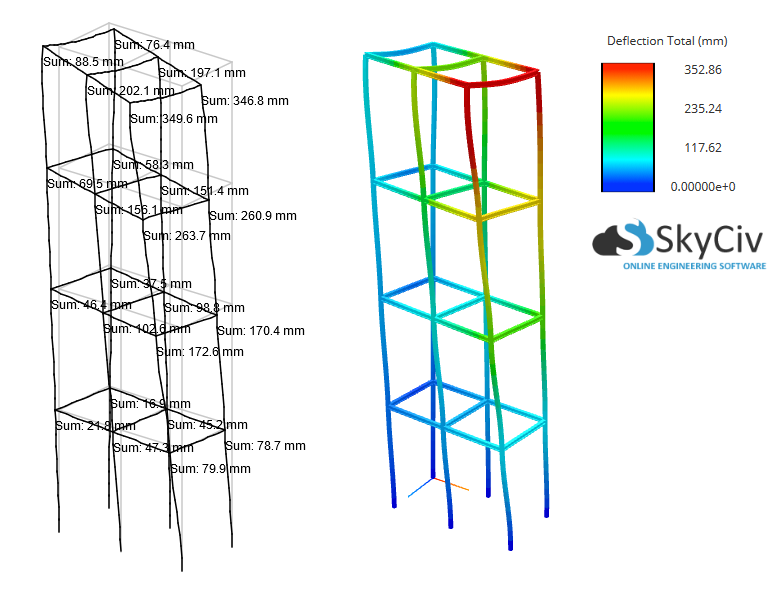Está claro que los efectos P-Delta juegan un papel extremadamente significativo con esta estructura, aumentando la desviación máxima y los resultados de momento máximo alrededor 40%! Así, un análisis estático lineal es inadecuado en tal caso. En resumen, El análisis P-Delta es preferible al análisis estático lineal, ya que explica las no linealidades imprevistas en su modelo. Puedes usar SkyCiv Structural 3D para realizar análisis P-Delta rápidos y efectivos en sus modelos; simplemente seleccione "Análisis P-Delta" al hacer clic "Resolver." Deje que el software haga el trabajo por usted, por lo que solo tiene que preocuparse por el diseño.!