P-Delta分析是一种分析类型，对于侧向承受重力载荷的多层建筑结构特别重要. 在这篇文章中, SkyCiv在线工程软件 将讨论P-Delta效应背后的简单理论，并帮助您理解在对结构建模时进行此类分析的重要性.  

什么是P-Delta效应?

当然, 任何结构模型在加载时都会发生变形. 挠曲的结构可能会遇到明显的二次弯矩，因为构件的端部已更改位置. 为了说明这一点, 考虑下面显示的简单悬臂列示例: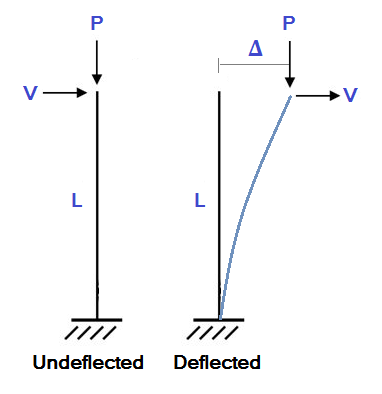 在这个例子中, 长度为L的圆柱承受轴向载荷 (P) 和横向载荷 (V). 在标准线性静力分析中，我们将计算侧向挠度 (Δ) 作为: [数学] \Delta = dfrac{ML ^ 2}{3不} = dfrac{VL ^ 3}{3不} \文本{ 由于M = VL} [数学] 注意，在线性静力分析的情况下，横向挠度, Δ, 取决于侧向载荷 (V). 然而, 如果柱子承受轴向载荷 (P), 那柱子会不会偏转得更多? 这是显而易见的，因为轴向载荷会引起二次力矩，其值为P×Δ. 为了说明这一点, 让我们总结一下有关该列基础的内容: [数学] \和{中号}=(V L) + (P 时间 Delta)= VL + P 三角洲 \\\\ M_{1} = VL \\\\ M_{2} = P Delta [数学] 这里M₁ 是由于侧向点载荷而, 中号₂ 是由于轴向载荷. 这些力矩中的每一个对侧向偏转的贡献都不同 (您可以查找由于点荷载和弯矩而引起的端部挠度的悬臂公式, 这些公式分别): [数学] \三角洲_{1} = dfrac{M_{1}L ^ 2}{3不} = dfrac{VL ^ 3}{3不} \\\\ \三角洲_{2} = dfrac{M_{2}L ^ 2}{2不} = dfrac{P Delta L ^ 2}{2不} [数学] 所以真的, 总的横向挠度将更接近: [数学] \三角洲_{新的} = Delta_{1} + \三角洲_{2} = dfrac{VL ^ 3}{3不} + \dfrac{P Delta L ^ 2}{2不} [数学] 我们可以看到与原始挠度值相比, 在右边有一个关于P和Δ的附加项. 如果P或Δ为有效值, 标准的线性静力分析会低估色谱柱的挠度. 现在应该显而易见的是，P-Delta分析是在次要时刻之后命名的 局部放电. 因此, P-Delta效应是由几何非线性引起的. 为此原因, P-Delta分析通常称为 非线性分析. 适当的P-Delta分析将继续重复上述过程以更新Δ的值_新的.

我什么时候需要担心进行P-Delta分析?

好消息是 SkyCiv结构3D 现在可以为您执行P-Delta分析. P-Delta效应通常在高层结构中普遍存在，这些高层结构由于风或其他作用力而承受重力载荷和横向位移. 如果通过结构的横向位移和/或垂直轴向载荷很大, 应该执行P-Delta分析以解决非线性问题. 在很多情况下, 线性静态分析可以 严重低估 移位 (除其他结果外) 与P-Delta相比 (非线性的) 分析. 下例将说明P-Delta非线性分析的重要性. 建筑物的多层框架高度为20m, 每层高5m. 立柱完全固定在基座上，每层上均分布有荷载. 另外, 顶层有垂直荷载，并考虑了自重，因此可以模拟重力荷载. 还有一个 相对较小 施加在结构侧面的侧向荷载.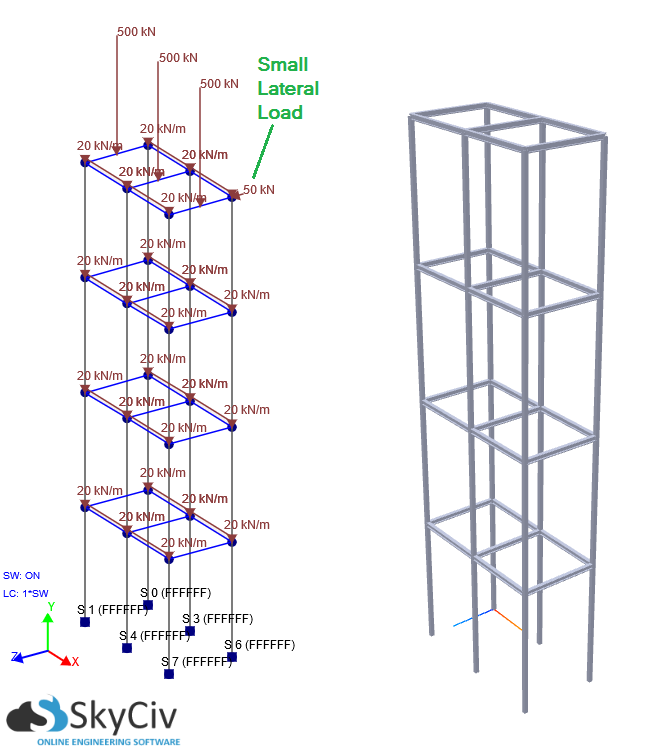   在这些条件下，让我们比较线性和P-Delta的结果 (非线性的) 分析:

	线性的	三角洲 (非线性的)	% 区别
最大总排量	254 毫米	353 毫米	+ 39%
最大垂直反应	629 千牛	668 千牛	+ 6%
最大矩反应	42 千牛·米	60 千牛·米	+ 43%

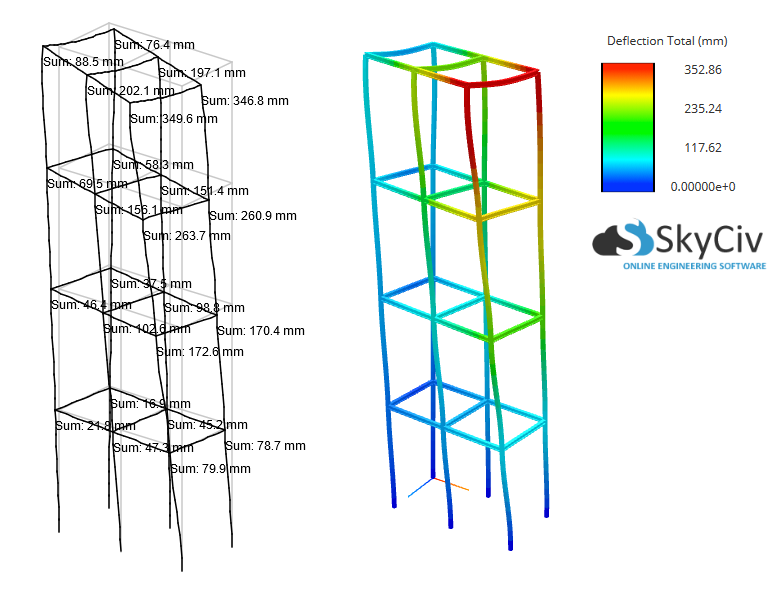显然，P-Delta效应在这种结构中起着极其重要的作用, 将最大挠度和最大力矩结果增加大约 40%! 从而, 在这种情况下，线性静态分析是不够的. 综上所述, P-Delta分析优于线性静态分析，因为它可以解决模型中不可预见的非线性问题. 您可以使用 SkyCiv结构3D 在模型上执行快速有效的P-Delta分析; 只需选择 "P-Delta分析" 点击时 "解决。" 让软件为您完成工作，所以您所要做的就是设计!  

免费注册