SkyCiv General Section Designer Verification for RC Sections

Information presented on this page is intended to demonstrate the section design convergence that can be achieved with SkyCiv.
All examples are taken from the REINFORCED CONCRETE DESIGN TO EUROCODE 2, SIXTH EDITION (authors BILL MOSLEY, JOHN BUNGEY, RAY HULSE). Current manual consists description of algorithm of manual calculations.
Example 4.5: Analysis of flanged section (stress block depth lies within the flange)
| Design Case | Manual | SkyCiv result | Manual / SkyCiv |
|---|---|---|---|
| Design moment strength M Rd, kN-m | 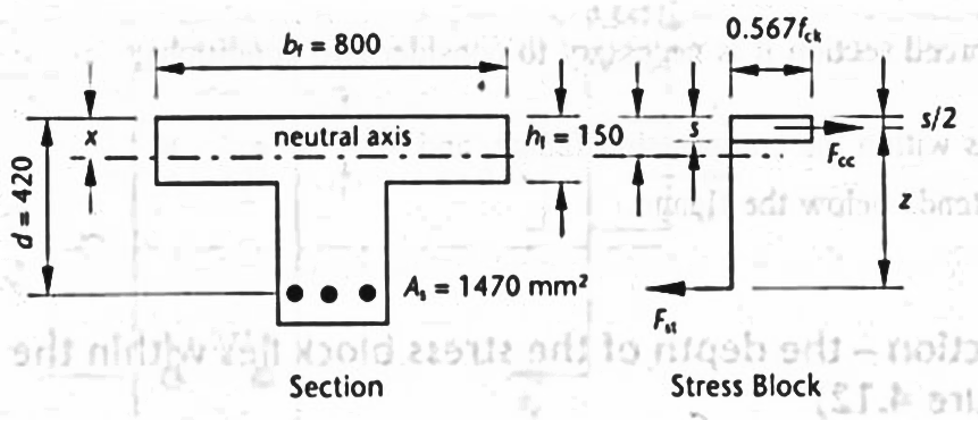 |
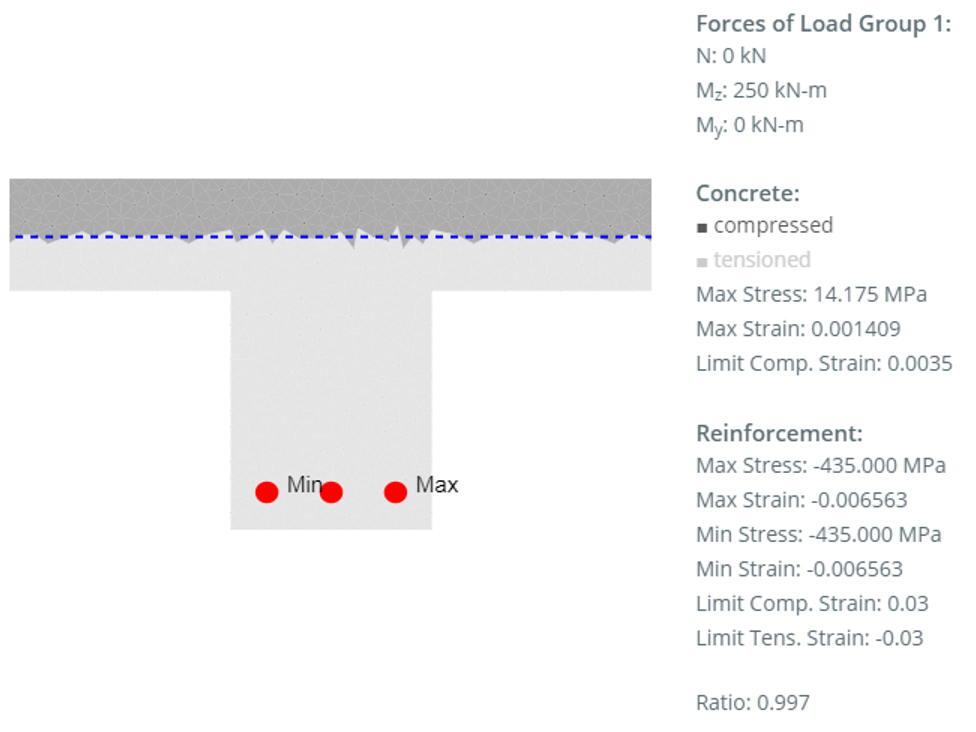 |
249.0 / 249.25 0.1% |
Example 4.7: Analysis of flanged section (stress block depth lies within the web)
| Design Case | Manual | SkyCiv result | Manual / SkyCiv |
|---|---|---|---|
| Design moment strength
M Rd, kN-m |
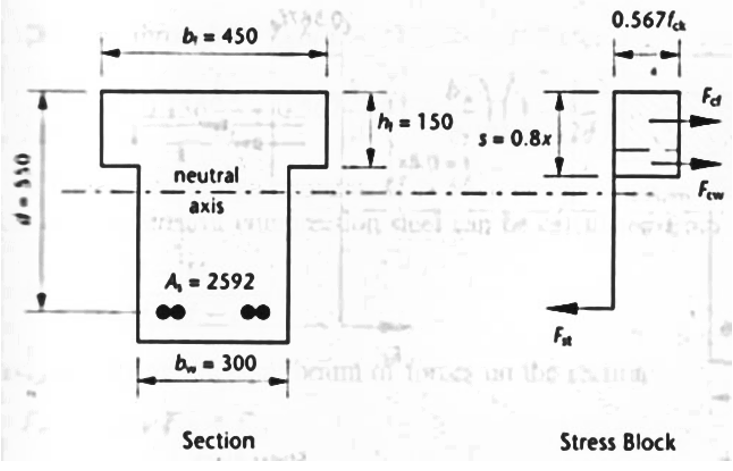 |
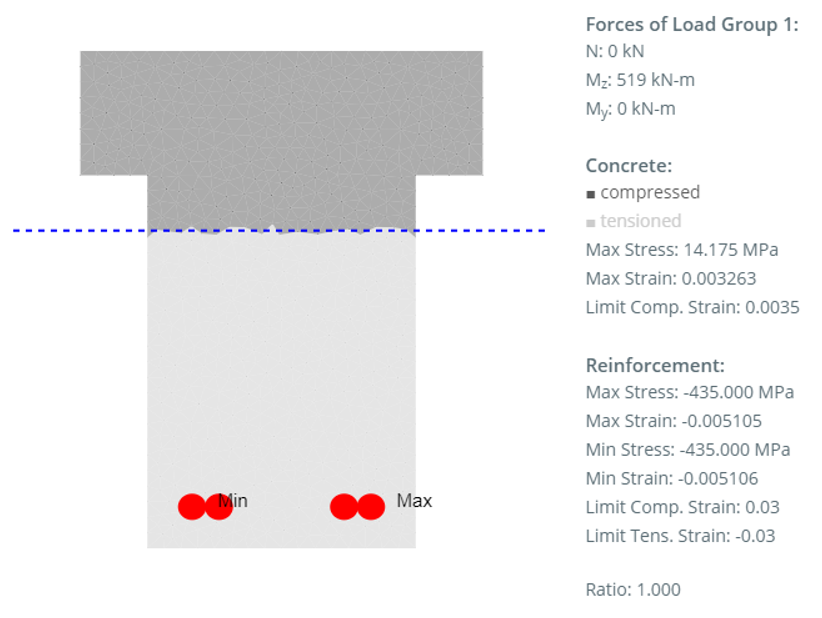 |
519.0 / 519.0 0% |
Example 4.10: M-N interaction diagram for non-symmetrical section
| Design Case | Manual | SkyCiv result |
|---|---|---|
| MRd – NRd curve | 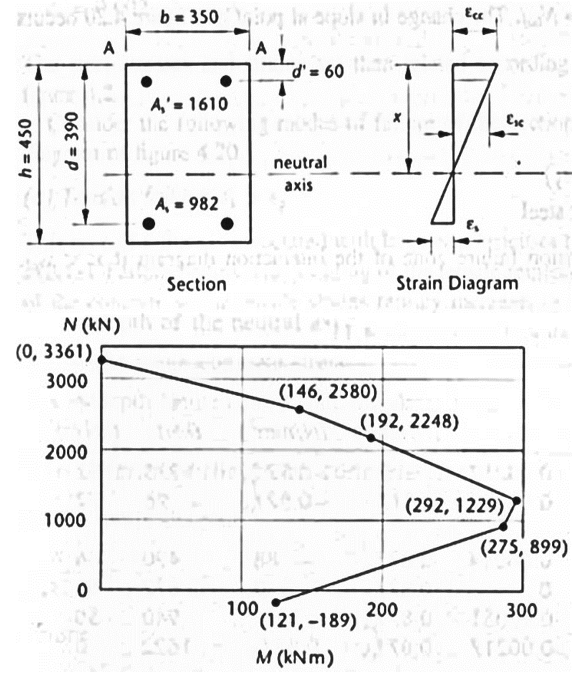 |
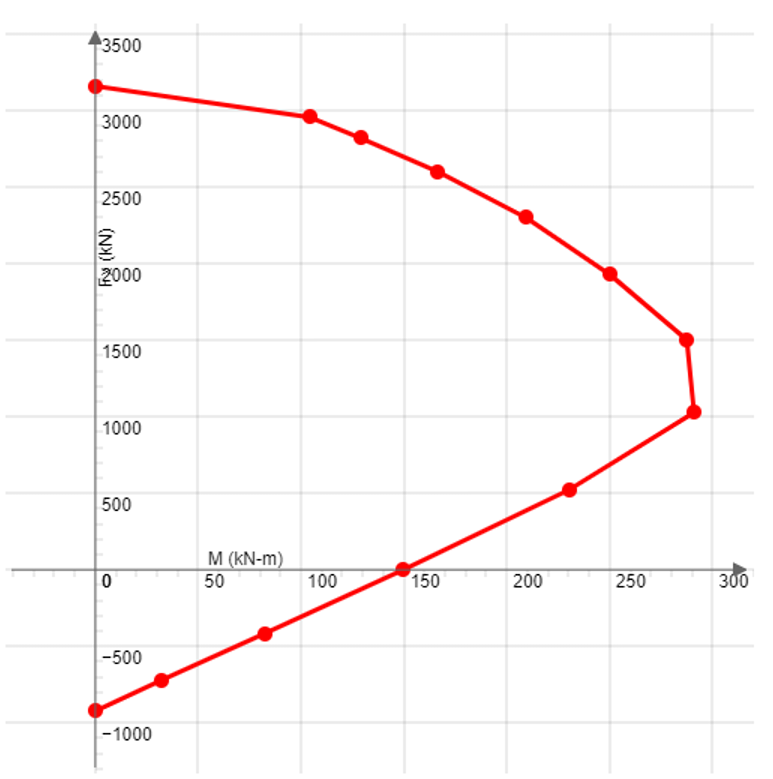 |
Example 4.11: M-N interaction diagram for a non-rectangular section
| Design Case | Manual | SkyCiv result |
|---|---|---|
| MRd – NRd curve | 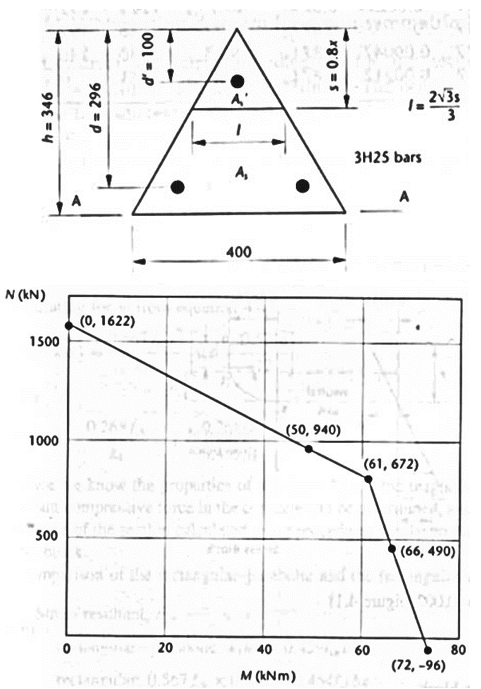 |
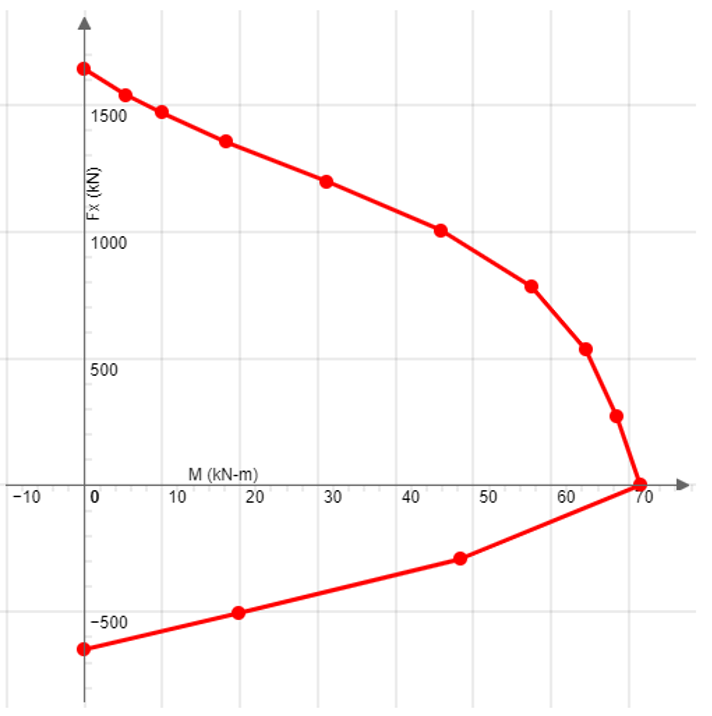 |

